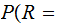 A
A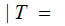 F
F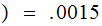 the
probability that A was received given that F
was transmitted.
the
probability that A was received given that F
was transmitted.
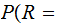 F
F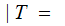 F
F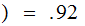 is
the most
probable.
is
the most
probable.
In the previous discussion of
Hamming Distance and Linear Codes, by assuming that there is at most a one bit
error in the transmission of a given letter code, we simplified the problem of
transmission error analysis. Probabilities had really only played a role when
we considered the table of letter Transmission frequencies in
our discussion of Huffman Codes.
Symbol
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
Probability
0.086
0.014
0.028
0.038
0.130
0.029
0.020
0.053
0.063
0.001
0.004
0.034
0.025
0.071
0.080
0.020
0.001
0.068
0.061
0.105
0.025
0.009
0.015
0.002
0.020
0.001
In the following discussion we will want to consider table above as a row
vector. Informally, the reason for this is that, assuming that there are
Channel errors, associated with each letter,say
F, there is a row vector of error
probabilities, possibly different for different letters:
Symbol
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
Probability
0.0015
0.0003
0.0012
0.0017
0.0032
0.9200
0.0022
0.0043
0.0013
0.0011
0.0024
0.0034
0.0025
0.0071
0.0080
0.0020
0.0001
0.0068
0.0013
0.0011
0.0024
0.0034
0.0025
0.0071
0.0080
0.0020
Where, for example
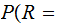 A
A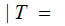 F
F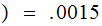 the
probability that A was received given that F
was transmitted.
the
probability that A was received given that F
was transmitted.
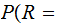 F
F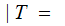 F
F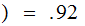 is
the most
probable.
is
the most
probable.
By considering the 26 error row vectors as a 26 by 26 matrix, we compute
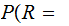 A
A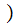 by
multiplying the "Transmission row vector" by the "Received A" column of the
error matrix.
by
multiplying the "Transmission row vector" by the "Received A" column of the
error matrix.
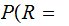 A
A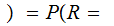 A
A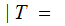 A
A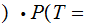 A
A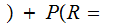 A
A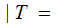 B
B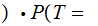 B
B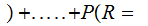 A
A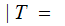 Z
Z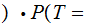 Z
Z
Below, I will reserve
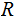 and
and
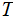 for the Random Variable associated with the English alphabet.
for the Random Variable associated with the English alphabet.
Using
the generic
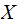 and
and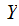 is an acknowledgement that the process we are interested in is more complex. ,
While
is an acknowledgement that the process we are interested in is more complex. ,
While
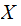 may
indeed be some familiar symbol set,
may
indeed be some familiar symbol set,
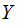 will
the the result of encoding and transmission. Below we formally introduce
will
the the result of encoding and transmission. Below we formally introduce
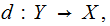 decoding/error detection/error correction.
decoding/error detection/error correction.
If
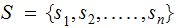 it will be convenient to reuse the symbol
it will be convenient to reuse the symbol
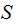 for
the "identity" Random Variable
for
the "identity" Random Variable
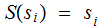 . Again, I am somehow assuming
. Again, I am somehow assuming
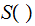 takes
numerical value. I am being a bit inprecise here.
takes
numerical value. I am being a bit inprecise here.
Definition: A Channel
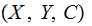 consists
of:
consists
of:
An input alphabet
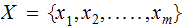
An output alphabet
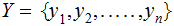
An m row by n column, Channel
Matrix.
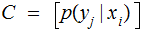 ,
where
,
where
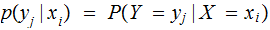 is the probability that
is the probability that
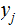 is
received, given that
is
received, given that
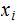 is transmitted.
is transmitted.
Explicitly, we are assuming
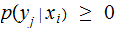 and
for each
and
for each
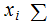
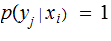
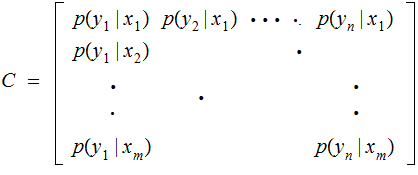
Note:
One can little about the sum of the various columns.
Without additional assumptions one can say nothing about any
symmetries.
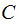 may
or may not equal
may
or may not equal
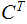 .
.
Definition:
A Channel
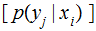 is called Symmetric if each row contains the same entries,
and each column contains the same entries, perhaps not in the same
order.
is called Symmetric if each row contains the same entries,
and each column contains the same entries, perhaps not in the same
order.
An Aside: This is confusing terminology. We
are saying the Channel is Symmetric, not the Matrix
(we are not claiming
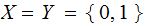 .
.
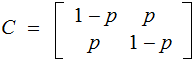
Exercise: Suppose we are transmitting 2 bits in parallel down two independent Binary Symmetric Channels with
channel matrices
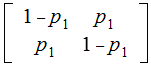 and
and
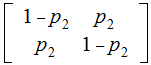 the input and output alphabets are both
the input and output alphabets are both
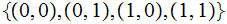
What is the channel matrix for this Channel? is it a Symmetric Channel?
We use the notation
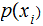 for
for
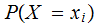 and
and
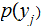 for
for
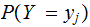 :
:
We are given a vector of input (read "Transmission" ) probabilities,
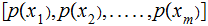 .
.
Again
explicitly,
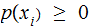 and
and
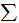
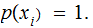
Hence we can compute the output (read "Reception") probabilities
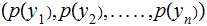

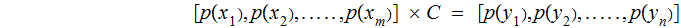

The Joint Probability Distribution:
 ,
where
,
where
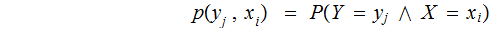
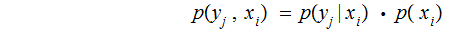

What can be said about the sums of rows, of columns, and of all
entries?
A Notational Isssue: The use of the notation
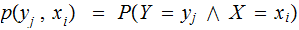 requires
some care:
requires
some care:
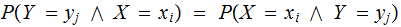 logically,
but
logically,
but
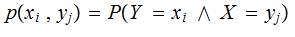 may
not even be a valid expression, the input and output alphabets may be
different. Even if they were the alphabets the same it may be the case that
may
not even be a valid expression, the input and output alphabets may be
different. Even if they were the alphabets the same it may be the case that
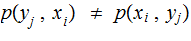

The Posterior Distribution
For a given vector of input probabilities,
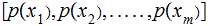
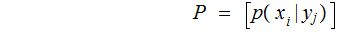 ,
where
,
where
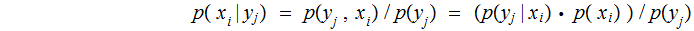
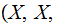
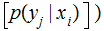 and
and
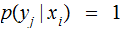 ,
,
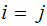
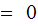 ,
,
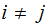
No Noise, verify that:
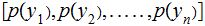
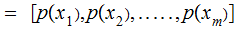
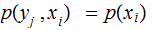 ,
,
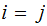
 ,
,
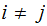
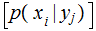
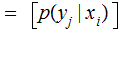
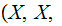
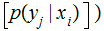 and
and
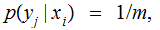 all
all
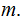

All Noise, verify that:
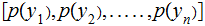
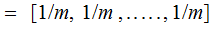 ,
,
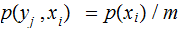 ,
all
,
all
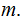

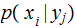
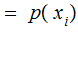 ,
knowing what was the output tells me nothing.
,
knowing what was the output tells me nothing.
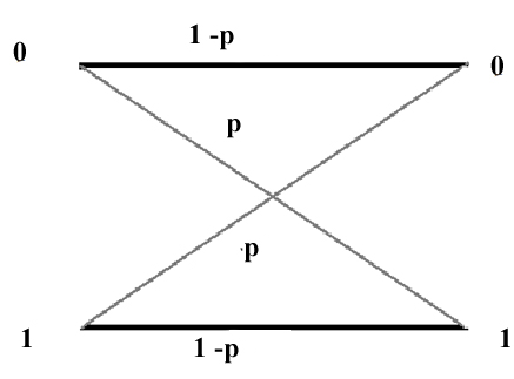
The Binary Symmetric Channel:
For an example let
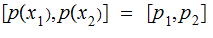
Exercise: Compute the Joint Probability Distribution and the Posterior
Distribution for a Binary Symmetric Channel.
Exercise: Again letting
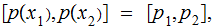 compute
the Joint Probability Distribution
compute
the Joint Probability Distribution
and the Posterior Distribution for a " Binary
Biased" Channel, defined by the matrix
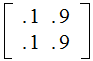
Definition: Given a
Channel 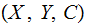 a Decoding Strategy is a function
a Decoding Strategy is a function
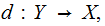 to be read, "Given that
to be read, "Given that
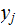 is
the output,
is
the output,
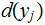 was the input.
was the input.
In general, Hamming Distance is not a Decoding Strategy, Why? What additional
relationships between code words is required to make it one?
Given a vector of input probabilities,
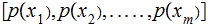 ,
the Maximum Likelihood Strategy
is:
,
the Maximum Likelihood Strategy
is:
Compute
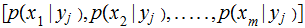 and Define
and Define
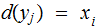 where
where
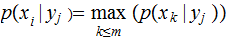
As defined, is the Maximum Likelihood Strategy really a strategy? What are the
issues?
Discuss the Maximum Likelihood Strategy as it relates to Examples 1. and 2.
above.
Discuss the Maximum Likelihood Strategy as it relates to Repetition
Codes.
For Further Analysis( See Notes): Relate the Hamming Distance Strategy to Maximum Likelihood. Strategy. Assume that the input and output alphabets are strings, of bits, of the same length and the probabilities of error for each bit is the same.