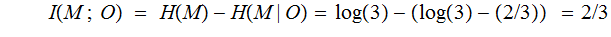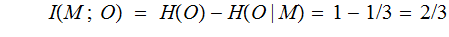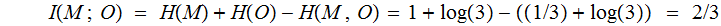 Hamming Code :
Hamming Code :
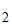 Hamming Code :
Hamming Code :
The matricies:
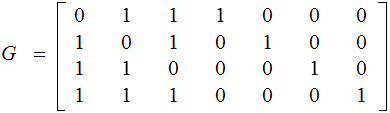 and
and
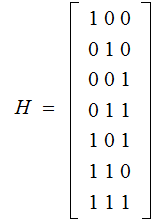
Again, given
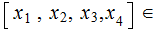
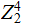 we
encode it by multiplying on the right by
we
encode it by multiplying on the right by
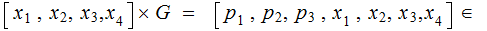

 If
If
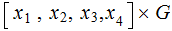 is correctly received
is correctly received
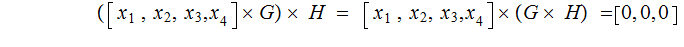
Let
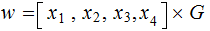 Suppose there is a single bit transmission error:
Suppose there is a single bit transmission error:
The vector received is of the form
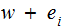 where
where
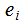
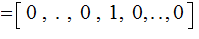 ,
,
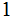 in
the
in
the 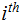 position
position
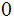 in every other position.
in every other position.
Since
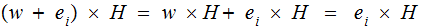 ,
which is just the
,
which is just the
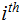 row of
row of
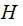 ,
the
,
the
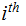 bit
is an error.
bit
is an error.
Definition:
Given a
Channel 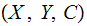 a Decoding Strategy is a function
a Decoding Strategy is a function
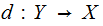 .
.
 To
be read, "Given that
To
be read, "Given that
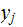 is
the output,
is
the output,
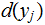 was the input.
was the input.
In general, Hamming Distance is not a Decoding Strategy, Why? What additional
relationships between code words is required to make it one?
Working in
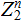 , the Hamming Distance Decoding Strategy would be, pick a set of code words.
For each code word map all words that are at most one bit away onto that code
word.
, the Hamming Distance Decoding Strategy would be, pick a set of code words.
For each code word map all words that are at most one bit away onto that code
word.
 where
where
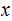 is a code word and
is a code word and
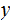 differs from
differs from
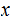 by at most one bit.
by at most one bit.
This is called The Hamming Ball of radius
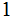 around
around
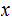 .
The problem is that, in general
.
The problem is that, in general
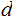 is not well defined because some words in
is not well defined because some words in
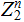 may not be within
may not be within
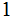 of a code word. Indeed sometimes there is no set of code words that avoids
this problem.
of a code word. Indeed sometimes there is no set of code words that avoids
this problem.
A good example is
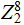 . The Hamming Ball of radius
. The Hamming Ball of radius
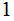 around any code word contains
around any code word contains
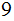 words. But there are
words. But there are
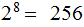 possible eight-bit words, and you can't divide
possible eight-bit words, and you can't divide
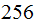 words into disjoint sets of
words into disjoint sets of
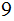 .
.
The Hamming Distance Decoding Strategy for the
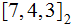 Hamming Code is a Perfect Code. The space of output code
words is
Hamming Code is a Perfect Code. The space of output code
words is
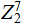 ,
,
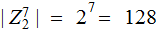 possible
code words. There are
possible
code words. There are
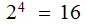 "error
free"
"error
free" codewords
(
codewords
( 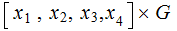 )
and The Hamming Ball of radius
)
and The Hamming Ball of radius
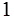 around any code word contains
around any code word contains
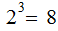 words and
words and
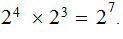
To give a formal definition of
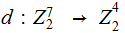 we
need
we
need
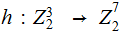 defined by ,
defined by ,
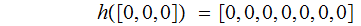
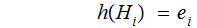 where
where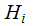 is
the
is
the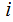 th row of
th row of
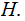
We also use
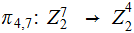 projection onto the last
projection onto the last
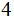 bits in
bits in
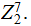
Define
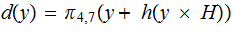
Given a vector of input probabilities,
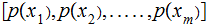 ,
the Maximum Likelihood Strategy is:
,
the Maximum Likelihood Strategy is:
Compute
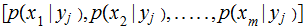 and define
and define
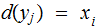 where
where
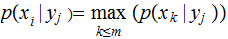
As defined, is the Maximum Likelihood Strategy really a strategy? What are the
issues?
No, since two code words might have the same maximum probability.
Suppose the probability of a single bit error is
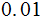 and that all bits are independent. The probability of a word being sent
correctly or with at most one bit error is
and that all bits are independent. The probability of a word being sent
correctly or with at most one bit error is
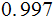
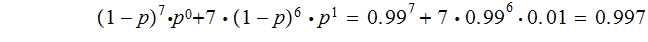
(Followup Exercise ) Compute
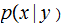 where
where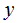 is
an error word, where
is
an error word, where
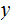 is
an valid code word.
is
an valid code word.
(Followup Exercise ) What can be said about the Hamming Ball Strategy and Maximum Likelihood Strategy for Perfect Codes
The above image is from MacKay's Lectures
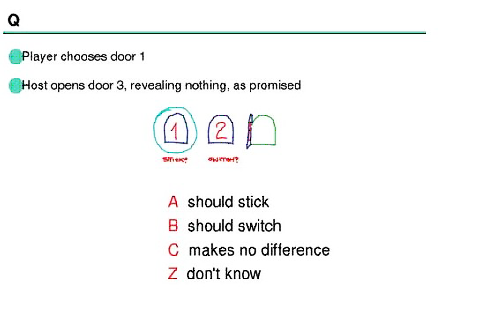
The Host hides a money prize behind one of three randomly chosen doors
.
The Player chooses a door, say 1.to simplify the discussion
of the problem. The essential calculation is not affected
.
The Host opens either door 2 or door 3 using the following rules:
If the money is behind door 1 open 2 or 3 at random, flip a coin.
If the money is behind door 2 open 3 and if it is behind 3 open 2.
The Question: Suppose the Host opens door 3, should the Player open door 1 or open door 2.?
The Random Variables:
The door that the money is hidden behind:
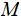 ,
which takes on the values
,
which takes on the values
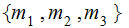 with
with
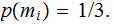
The door that the Host opens
 ,
which takes on the values
,
which takes on the values
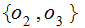
Given 1., we would predict that
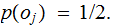 see
below
see
below
The Conditional Distribution:
In 3. of the Description above, we are not given a joint probability
distribution, we are given a conditional probability distribution
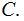
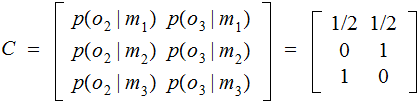
Some notes:
Check that
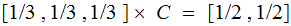
If
the money prize is hidden using a uniform distribution the door opened is a
uniform distribution.
Is there a Shannon Clue in the facts that
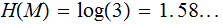 and
and
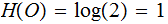 ?
?
The Three Door Problem logic can be considered anologous to Noisy Channel
logic. The input alphabet is
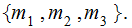
The output alphabet is
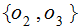 ,
the channel matrix is
,
the channel matrix is
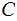 , and we given the output, the door opened, weare asked to infer the input,
where the prize is.
, and we given the output, the door opened, weare asked to infer the input,
where the prize is.
.
The door that the Player chooses is NOT a Random Variable it is a Decoding
Strategy
The Posterior Distribution:
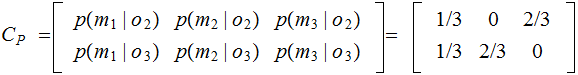
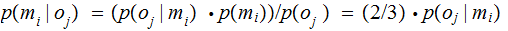
Read: Given that door 3 is opened The probability that it is behind door 1 is
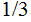 ,
door 2 is
,
door 2 is
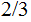 and
door 3 is
and
door 3 is
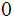 .
.
The Decoding Strategy:
Using the Maximum Likelihood Strategy,
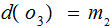 and
and
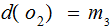
. The Joint Distribution:
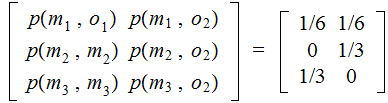
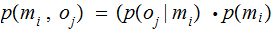
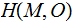
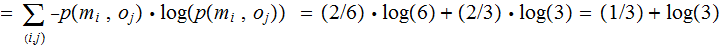
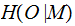 ,
,
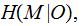 and
and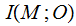
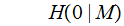
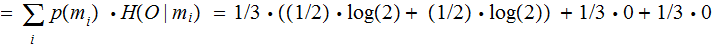
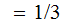
Using Row Symmetry:
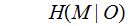
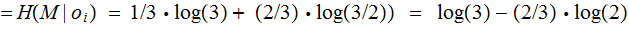
Finally