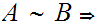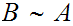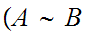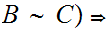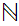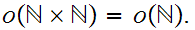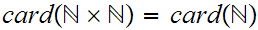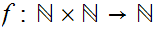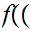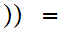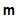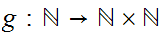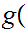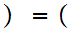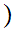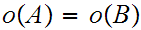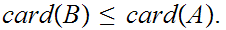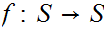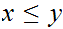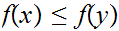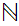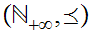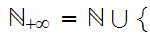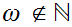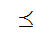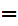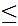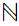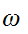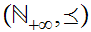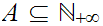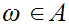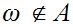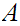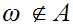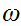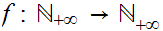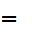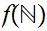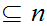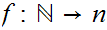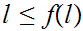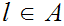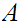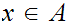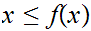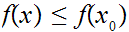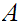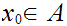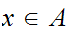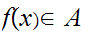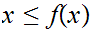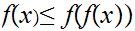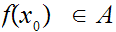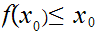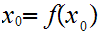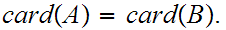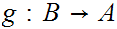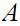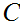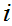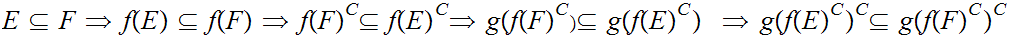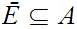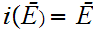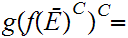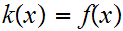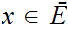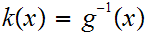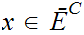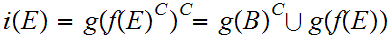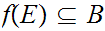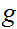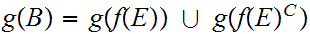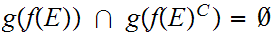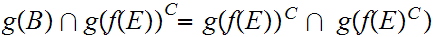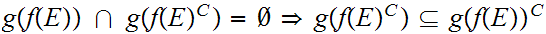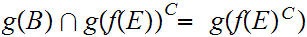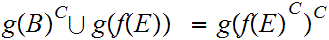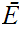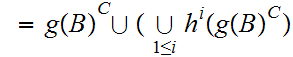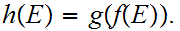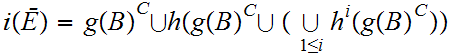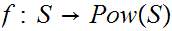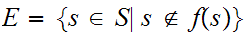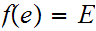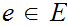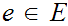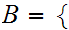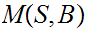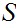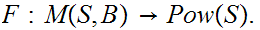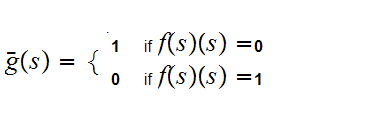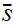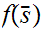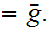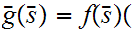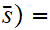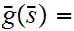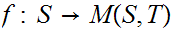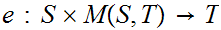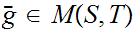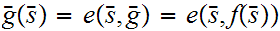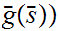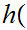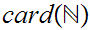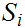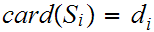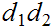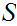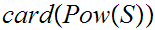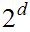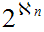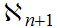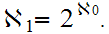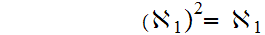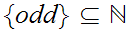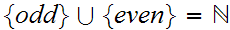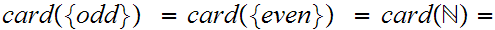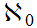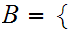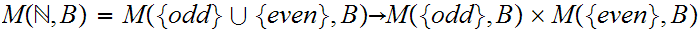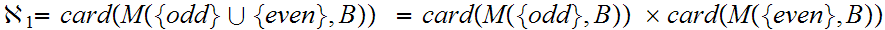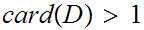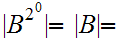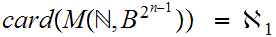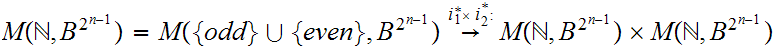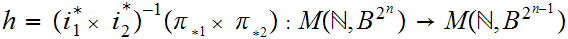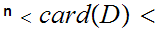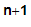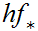9. Cardinal Numbers
The
size of sets:
We want to extend the notion of size of finite sets that is provided by the
natural numbers so that we can compare the "size" of any two sets. It is worth
noting that the following definition requires some reassurance that we are on
mathematically firm ground since we are certainly on the edge of Russell
territory. We will discuss this further when we consider alternatives to ZF
set theory.
9.1
Definitions:
-
Let
 be the equivalence relation on the "class" of all set defined by
setting
be the equivalence relation on the "class" of all set defined by
setting  if there exists a 1 to 1 onto map
if there exists a 1 to 1 onto map
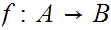 .
This is the books notation.
.
This is the books notation.
-
We define a second equivalence
relation 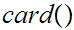 on the class of all set by
setting
on the class of all set by
setting  if there exists a 1 to 1 map
if there exists a 1 to 1 map
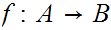 and a 1 to 1 map
and a 1 to 1 map
 .
.
-
Finally, we
write  if the exist a 1 to 1
map
if the exist a 1 to 1
map 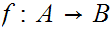 .
.
Exercise: Check that 1. and 2. are
equivalence relations. For reference, you need to verify that

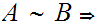
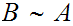
and
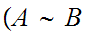 and
and
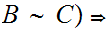

Observation:
For
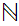 and
its subsets, we have essentially shown, that
and
its subsets, we have essentially shown, that
 iff
iff

We used this to also show that
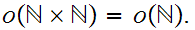 Note
that if we only wanted to show that
Note
that if we only wanted to show that
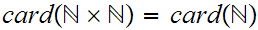 ,
it would have sufficed to present two one to one maps,
,
it would have sufficed to present two one to one maps,
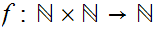 defined by
defined by
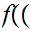 m,n
m,n 2
2 3
3
and
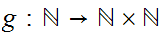 defined
by
defined
by
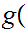 m
m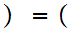 m,1
m,1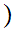
Goals:
-
We show that, in general, for any pair of sets
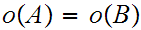 iff
iff

-
We also will show that for any pair of
sets,  or
or
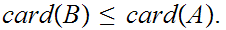
First, the following useful theorem.
9.2 The Tarski Fixed Point Theorem.
Let
 be a partially ordered set in which every non-empty sub-set has a least upper
bound and a greatest lower bound. If
be a partially ordered set in which every non-empty sub-set has a least upper
bound and a greatest lower bound. If
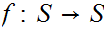 is order-preserving, that is
is order-preserving, that is
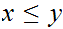 implies
implies
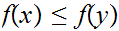 ,
then
,
then
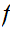 has a fixed point (
has a fixed point (
 ).
).
Proof.
Before proceeding with the proof. We look at two examples:
Examples:
1.
 - The map
- The map
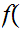 n
n n+1 has no fixed point. On the other hand,
n+1 has no fixed point. On the other hand,
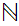 ,itself a subset, does not have a least upper bound.
,itself a subset, does not have a least upper bound.
2.
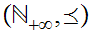
 -
where,again,
-
where,again,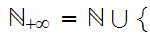
 ,
,
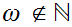 and
and
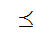
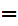
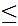 ,the usual ordering, on
,the usual ordering, on
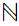 and n
and n

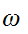 for
all
n
for
all
n
First, note that
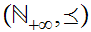
 satifies
the hypothesis of Tarski. To see this let
satifies
the hypothesis of Tarski. To see this let
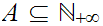 .
If
.
If
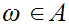 then it is the least upper bound (and the top element). If
then it is the least upper bound (and the top element). If
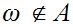 and
and
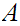 is
finite then it, as a finite subset of
is
finite then it, as a finite subset of
 ,
has a least upper bound( and again a top element). Finally, if
,
has a least upper bound( and again a top element). Finally, if
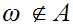 and
and
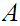 is
not finite,
is
not finite,
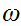 is the least upper bound, in fact the only upper bound( but not the top
element)
is the least upper bound, in fact the only upper bound( but not the top
element)
Next, to see that the conclusion of Tarski holds, let
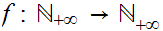 be order preserving. If
be order preserving. If

 we have our fixed point. If
we have our fixed point. If

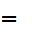 n
for some n then
n
for some n then
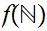
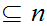 ,since
,since
 is
assumed to be order preserving.
is
assumed to be order preserving.
Finally, an induction argument shows that, in general, any order preserving
map
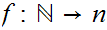 has a fixed point.
has a fixed point.
Let
 .
Then by definition,
.
Then by definition,
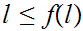 .
Let
.
Let
 Since
Since
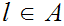 ,
,
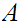 is
is
non-empty. Hence
 exists. For any
exists. For any
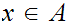 we have
we have
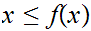
and
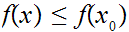 ,
so
,
so
 is an upper bound for
is an upper bound for
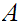 . Thus
. Thus
 and
and
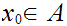
But, in general, if
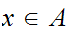 then
then
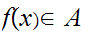 because
because
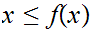 implies
implies
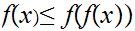 . Thus
. Thus
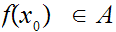 and
and
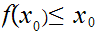
Finally, we conclude that
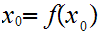 .
.
9.3 Theorem(Schroder-Bernstein)
For any pair of sets
 iff
iff
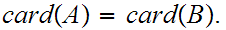
Proof.
By hypothesis, there exist one-to-one functions
 and
and
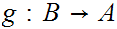 .
We apply the Fixed Point Lemma to the poset
.
We apply the Fixed Point Lemma to the poset
 and the function
and the function
 where
where
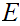
 .
Here the exponent
.
Here the exponent
 signifies Set complement.
signifies Set complement.
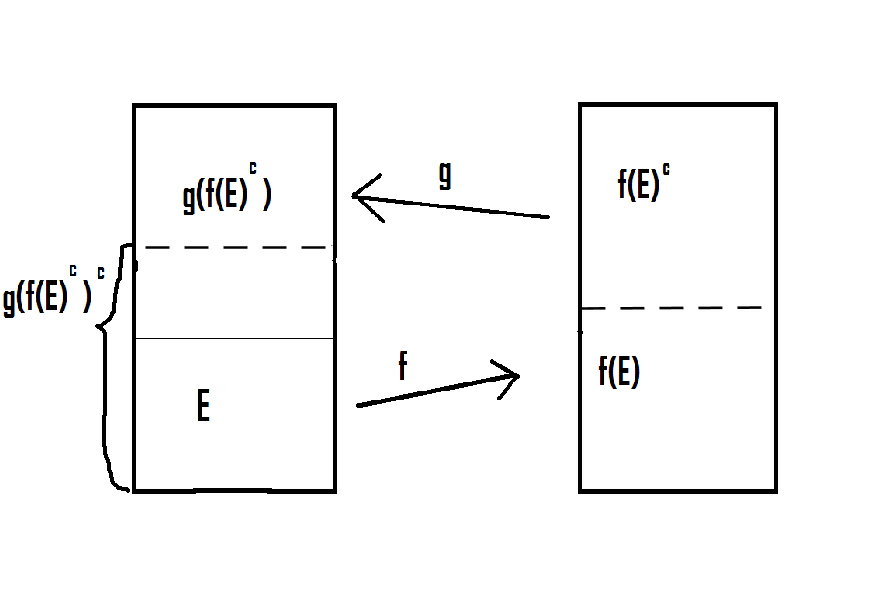
Note that
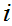 is order-preserving
is order-preserving
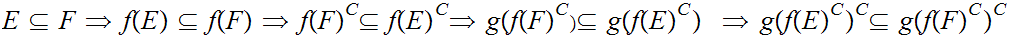
Hence, by the Tarski Fixed Point
Theorem, there is a set
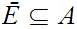 such that
such that
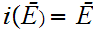
Specifically
,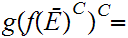

We can now define a 1 to 1 onto map
 by
by
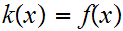 ,
,
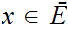 and
and
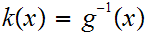 for
for
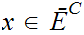 .
.
Two
Computations:
9.3.1 Lemma: In the setting of the Proof of
9.3
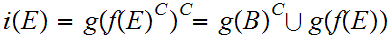 , the union being disjoint.
, the union being disjoint.
Proof.
That the union is disjoint simply follows from the fact that
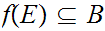 .
In addition, since
.
In addition, since
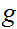 is one to one we also can write
is one to one we also can write
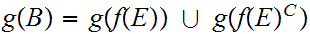 , with
, with
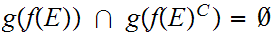 . Intersecting both sides with
. Intersecting both sides with
 gives
gives
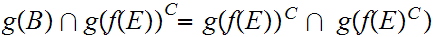
But
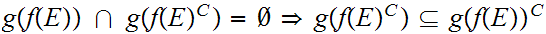
and thus
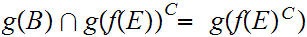
or, taking the complements of both sides
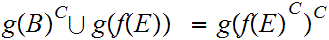
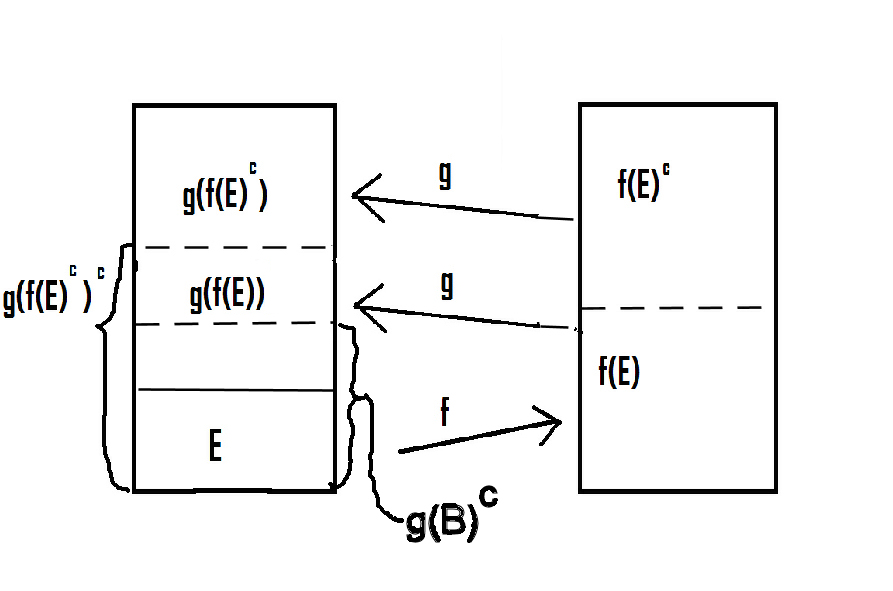
9.3.2 Theorem:
In the setting of the Proof of 9.3,
then 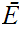
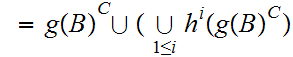
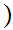 ,
,
where
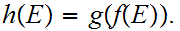 Moreover
the union is a disjoint union of non empty sets.
Moreover
the union is a disjoint union of non empty sets.
Proof.
From 9.3.1
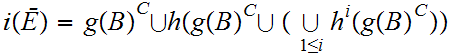

That the sets are disjoint follows from the fact that
 and
and
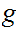 ,
hence
,
hence
 ,are one to one
,are one to one
More
Computations:
The hierarchy of cardinals:
We are now about ready to move to a more general discussion of set theory and
cardinals. We begin by noting that a more general discussion is appropriate by
showing that there are other cardinalities to be considered other than that of
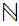 and its finite subsets .
and its finite subsets .
9.4 Theorem:
For any set
 ,there is no onto map
,there is no onto map
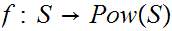 .
.
Proof A:( yet another diagonal argument. This is just
Russell's argument in a non-paradoxical setting)
Let
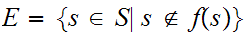 .
Since
.
Since
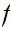 is onto there is some
is onto there is some
 with
with
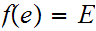 .
.
As usual, by definition if
 then
then
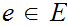 and if
and if
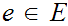 then
then
 .
.
Proof B:( yet another diagonal argument. This is just a
disguised version of A.)
Let
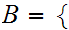 0,1
0,1 .
Let
.
Let
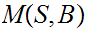 be the set of all maps from
be the set of all maps from
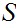 to
to
 . There is an obvious 1 to 1 onto map
. There is an obvious 1 to 1 onto map
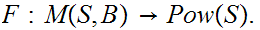 Specifically,
Specifically,
 1
1 . Hence to prove 9.4 we can show that for any set
. Hence to prove 9.4 we can show that for any set
 ,there is no onto map
,there is no onto map
 .
.
Suppose there was such a map. Define
 by the formula
by the formula
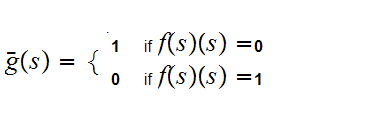
![$\vspace{1pt}$]() The
rest of the proof is standard. Suppose there was some
The
rest of the proof is standard. Suppose there was some
 such that
such that
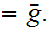 Compute
Compute
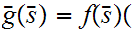
 If
If

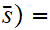 0
then by definition
0
then by definition
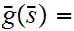 1
and so on.....
1
and so on.....
Proof C:( yet another fixed point theorem. )
We first prove the following lemma, which is really a generalization of
B.
9.4.1 Lemma : For sets
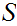 and
and
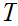 , suppose
there exists an onto map
, suppose
there exists an onto map
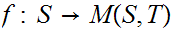 ,
then every self-map
,
then every self-map
 has
a fixed point.
has
a fixed point.
Proof:
Consider the "evaluation" map
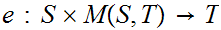 defined by the formula
defined by the formula

Like in B, above define
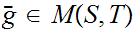 by the formula
by the formula

Again, since
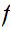 is onto there is some
is onto there is some
 such that
such that
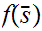

We have
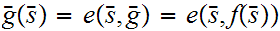
on the other hand, by definition,

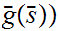
Thus
 is a fixed point for
is a fixed point for

Now, to complete the proof of 9.4, Let
 0,1
0,1 and note that
and note that
 has a fixed point free self-map. In particular, let
has a fixed point free self-map. In particular, let
 be define by the formula
be define by the formula
 0
0 1
and
1
and
 1
1 0
.
0
.
Notation:
-
The standard notation for
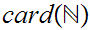 is
is
 .
.
-
For
 ,
if
,
if
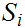 is a set with
is a set with
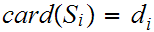 we use multiplicative notation
we use multiplicative notation
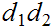 for
for
 Check that this is well defined.
Check that this is well defined.
-
If
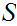 is a set with
is a set with
 ,
the standard notation for
,
the standard notation for
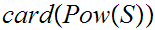 is
is
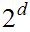 ,
as suggested by the second proof of 9.2 .
,
as suggested by the second proof of 9.2 .
-
The standard notation for
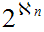 is
is
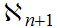
We will be very interested in
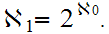 We end this Page with a Theorem that is in fact a special case of a general
result about infinite cardinals.
We end this Page with a Theorem that is in fact a special case of a general
result about infinite cardinals.
9.4 Theorem:
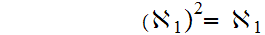
Proof:
Let
 and
and
 be the odd and even natural numbers respectively. In full detail,
be the odd and even natural numbers respectively. In full detail,
Again, letting
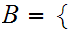 0,1
0,1 We invoke Lemma a. on the Background Page to observe
that there is a one-one onto map.
We invoke Lemma a. on the Background Page to observe
that there is a one-one onto map.
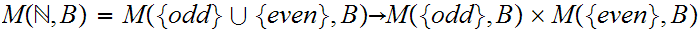
Hence,
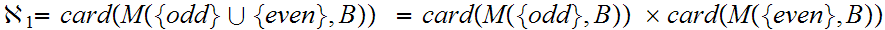

9.5 Theorem: Assignment to
be turned in:
Let
 be a finite set with
be a finite set with
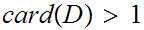 ,
then
,
then
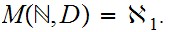
Hint:
Use Lemma 0.3 b. on the Background Page and
9.4 above to prove the theorem by induction for
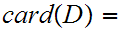 2
2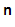 .
.
Next use 9.3 to prove the result when
2 2
2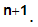
Solution
One verifies that
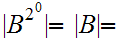 2
2
and
 2
2
By induction, suppose we have shown that
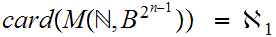
The map
 is one to one and onto.
is one to one and onto.
Similarly
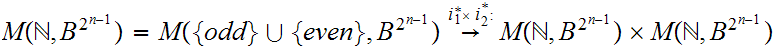 is one to one and onto.
is one to one and onto.
Thus
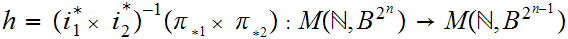 is one to one and onto.
is one to one and onto.
Now assume
2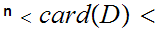 2
2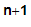 and choose one to one maps
and choose one to one maps
 and
and
 These
induce one to one maps.
These
induce one to one maps.
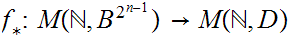 and
and

Finally, apply Schroder-Bernstein to
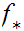 and
and
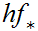 .
.
 be the equivalence relation on the "class" of all set defined by
setting
be the equivalence relation on the "class" of all set defined by
setting  if there exists a 1 to 1 onto map
if there exists a 1 to 1 onto map
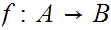 .
This is the books notation.
.
This is the books notation.
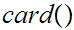 on the class of all set by
setting
on the class of all set by
setting  if there exists a 1 to 1 map
if there exists a 1 to 1 map
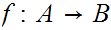 and a 1 to 1 map
and a 1 to 1 map
 .
.
 if the exist a 1 to 1
map
if the exist a 1 to 1
map 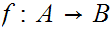 .
.