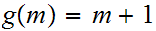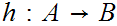 from
from
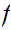 and
and
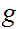 Here are two simple examples:
Here are two simple examples:
Two Examples:
The previous proof is "constructive" in that it actually provides us with an
algorithm that allows us to "compute"
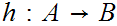 from
from
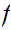 and
and
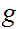 Here are two simple examples:
Here are two simple examples:
1.
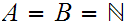 and
and
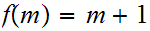 and
and
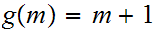
Start with
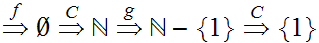
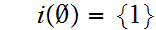
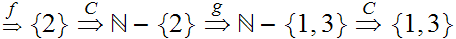
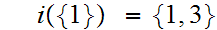

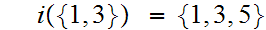
Hence, by "induction"
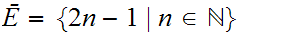 Verify
that this works. That is
Verify
that this works. That is
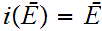 .
.
Now, define
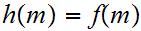 on
on
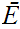 ,
and
,
and
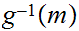 on
on
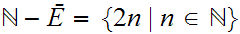
2.
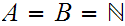 and
and
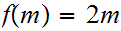 and
and
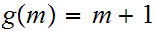
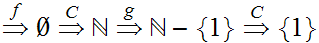
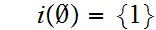
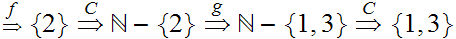
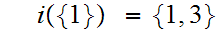
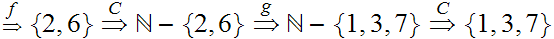
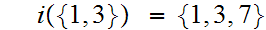
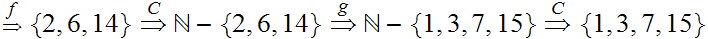
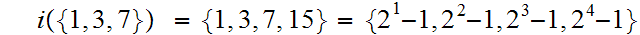
Hence, again by "induction"
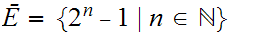 Verify that
Verify that
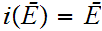 .
.
Exercise:
The Warmup.
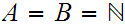 ,
,
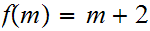 and
and
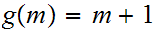
The Challenge:
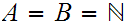
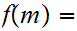
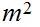
and