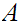 be
Well Ordered
be
Well Ordered
12.1 Theorem:
Let
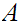 be
Well Ordered
be
Well Ordered
If
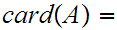 n then
n then
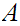 is order isomorphic to
is order isomorphic to
 .
.
or
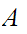 is
order isomorphic to
is
order isomorphic to
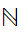
or
For some
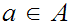 ,
,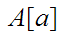 is
order isomorphic to
is
order isomorphic to
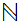 .
.
Proof:
By induction, if
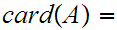 1 then the Theorem is immediate. Suppose the result holds for
1 then the Theorem is immediate. Suppose the result holds for
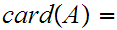 n-1. Let
n-1. Let
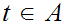 be the top element. The is an order isomorphism
be the top element. The is an order isomorphism
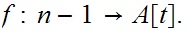 Extend
Extend
 to
to
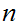 by setting
by setting
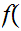 n
n .
.
Again, by induction, one shows that for n
 there a unique
there a unique
 such
that
such
that n.
Hence by 1. one has order isomorphisms
n.
Hence by 1. one has order isomorphisms
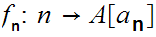 .
Checking that
.
Checking that
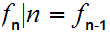 we have an order isomorphism
we have an order isomorphism
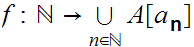 .
Either
.
Either
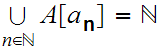 .
.
or
 where
where
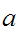 is
the least element of
is
the least element of
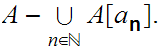
In more generality.
12.2 Theorem:
Let
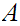 be
Well Ordered then the only self-order isomorphism
be
Well Ordered then the only self-order isomorphism
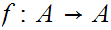 is the identity map.
is the identity map.
Proof:
Suppose
 is not the identity map. Let
is not the identity map. Let
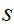 be
the least member of
be
the least member of
 such
that
such
that
 .
.
The segment mapping formula tell us that

but by assumption
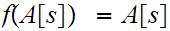 hence
hence
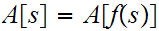 and
thus by 11.1.1
and
thus by 11.1.1
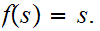
12.2 Corollary:
Let
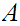 and
and
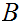 be Well Ordered and order isomorphic then the order isomorphism
be Well Ordered and order isomorphic then the order isomorphism
 is unique.
is unique.

Let
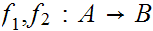 be two order isomorphisms.
be two order isomorphisms.
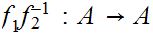 is a self-order isomorphism, hence the identity map,
is a self-order isomorphism, hence the identity map,
 .
Thus
.
Thus
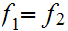 .
.
12.3 Theorem:
Let
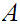 be Well Ordered and let
be Well Ordered and let
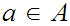 ,
, there is no order isomorphism
there is no order isomorphism
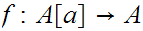 .
.
Proof:
Suppose there was an order isomorphism
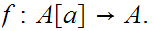
Since
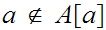 there exists some
there exists some
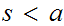 such that
such that
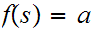 In particular
In particular
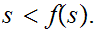
Let
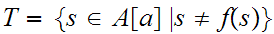 .
Since
.
Since
![$\QTR{Large}{A[a]}$](graphics/WellOrdered12__56.png) is Well Ordered let
is Well Ordered let
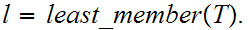
Thus
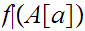
![$\QTR{Large}{[l]}$](graphics/WellOrdered12__59.png) is the identity map. Restated
is the identity map. Restated
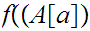
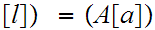
![$\QTR{Large}{[l].}$](graphics/WellOrdered12__62.png) But
But



 . Thus
. Thus
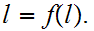 ,
contradicting the definition of
,
contradicting the definition of
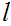 .
.
12.4 Lemma:
Let
 be Well Ordered. Let
be Well Ordered. Let
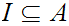 be an Ideal Cut, then
be an Ideal Cut, then
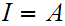 or for some ,
or for some ,
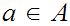 ,
,
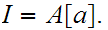
Proof:
If
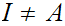 ,
let
,
let

12.5 Theorem:
Let
 and
and
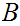 be
Well Ordered then
be
Well Ordered then
 is order isomorphic to a segment of
is order isomorphic to a segment of
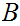 .
.
or
 is
order isomorphic to a segment of
is
order isomorphic to a segment of
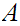 .
.
or
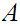 and
and are
order isomorphic.
are
order isomorphic.
Proof:
Consider the Set of triples
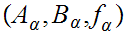 where
where
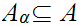 and
and
 are Ideal Cuts and,
are Ideal Cuts and,
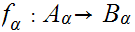 is an order isomorphism.
is an order isomorphism.
We let
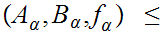
 if
if
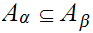

and
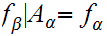
Exercise(due Wed. March 29) Show that this is an ordered Set. (Hint: use 12.2).
Assuming this, Consider the triple
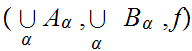 where
where
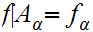 .
Again, one checks that this is an order isomorphism.
.
Again, one checks that this is an order isomorphism.
Clearly the triple is maximal with respect to the three bullets. In
particular,
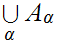 and
and
 are Ideal Cuts (11.1.2). Thus by
12.4 ,
are Ideal Cuts (11.1.2). Thus by
12.4 ,
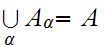 ,
,
 or both are segments and we can then extend
or both are segments and we can then extend
 a contradiction.
a contradiction.
On the next Page we will want a "constructive" version of the material just presented. In particular, we will extract Well Ordered subsets of posets. Here are the details.
We are given a poset

 .
We restrict attention to
.
We restrict attention to
 , the Well Ordered subsets.
, the Well Ordered subsets.
Definition 12.6:
A subset
 is called "complete" if
is called "complete" if
 and
and
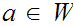 implies
implies
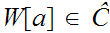 . That is if a Well Ordered subset is in
. That is if a Well Ordered subset is in
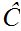 so are all its segments. Clearly
so are all its segments. Clearly
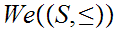 itself is complete.
itself is complete.
Note: Implicit in the definition is the assumption that
 is
Well Ordered, "vacuously".
is
Well Ordered, "vacuously".
If you are uncomfortable with this assumption, just define "complete" on
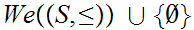 .
.
Note: One also finds these subsets called "good" or "special."
Theorem 12.7:
Fix
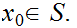 Let
Let
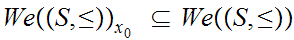 be the set of Well Ordered subsets with least element
be the set of Well Ordered subsets with least element
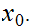 Let
Let
 be complete and such that there exists a function
be complete and such that there exists a function
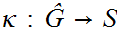 with the property that
with the property that
 for all
for all
 and
and
 then
then
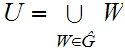
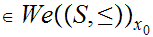 .
.
Proof:
One needs to show that to show that if
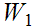 and
and
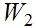 are in
are in
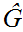 then
then
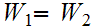 ,
,
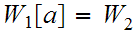 for some
for some
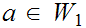 , or
, or
 for
some
for
some
 .
.
As we noted before, in that case,
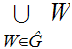 is Well Ordered
is Well Ordered
Let
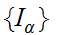 be
the set of common Ideal Cuts of
be
the set of common Ideal Cuts of
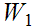 and
and
 . From the hypothesis
. From the hypothesis
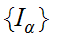 is
not empty. Hence
is
not empty. Hence
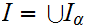 is common Ideal Cut of
is common Ideal Cut of
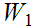 and
and
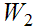 . Hence
. Hence
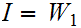 or
or
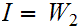 or
both, or
or
both, or
 is
a segment of both. But, suppose
is
a segment of both. But, suppose
there exists
 and
and
 such that
such that
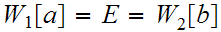 .
.
But
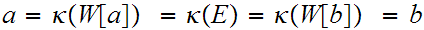 a contradiction since then
a contradiction since then
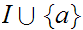 would
be a common Ideal Cut.
would
be a common Ideal Cut.
Examples:
1. For
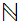 ,
let
,
let
 2.
Let
2.
Let
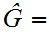
 finite
sequences of all even numbers beginning with 2 and ending
with 2n for some
n
finite
sequences of all even numbers beginning with 2 and ending
with 2n for some
n Clearly
Clearly
 is complete. Let
is complete. Let
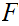
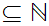 be any finite set. Define
be any finite set. Define
 Exercise Check that
Exercise Check that
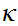 satisfies the hypothesis of 12.7 for
satisfies the hypothesis of 12.7 for
 Compute
Compute
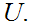
2.
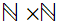 where
where
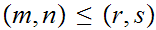 iff
iff
 and
and
 .
Let
.
Let
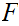
 be a chain. Define
be a chain. Define
 Exercise
Find the appropriate
Exercise
Find the appropriate
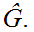 Compute
Compute

In discussing ordinal arithmetic it will be helpful to use a more precise notation for Well Ordered Sets.
12.8 Definition: Let
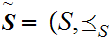
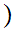 and
and

 be two Well Ordered sets with ,
be two Well Ordered sets with ,

 .
We define a Well Ordering
.
We define a Well Ordering

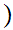 by the following three properties.
by the following three properties.

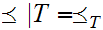
 for
for
 and
and
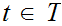 .
.
One checks
12.9 Theorem:
Let

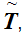 be
well ordered with
be
well ordered with
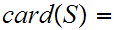 n
and
n
and 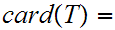 m, then, under the appropriate assumptions of
disjointness,
m, then, under the appropriate assumptions of
disjointness,
 is order isomorphic to
is order isomorphic to
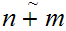 .
.
Let
 be order isomorphic to
be order isomorphic to
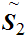 ,
,
 be order isomorphic to
be order isomorphic to
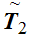 ,
,
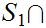
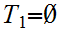 ,
and
,
and
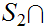
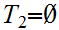 ,
then
,
then
 is
order isomorphic to
is
order isomorphic to
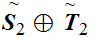 .
.
As we have seen, in general,
 is not order isomorphic to
is not order isomorphic to
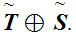
Look at
 and
and
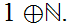
12.11
Definition: Let
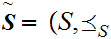
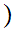 and
and
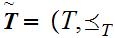
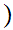 be two Well Ordered sets. We define a Well Ordering
be two Well Ordered sets. We define a Well Ordering

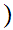 using "alphabetic order" as follows:
using "alphabetic order" as follows:
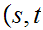


if

and if
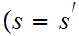
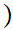
 if
if


Exercise: Check that this is a Well Order (Due Wed. March 29)
12.12 Observation:
In general,
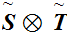 is not order isomorphic to
is not order isomorphic to
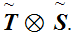
Look at
 and
and
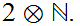
Exercise: How about

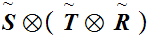
(Due Wed. March 29)
Solution:
The strategy is to write down the two definitions of order and observe that they are equivalent.
|
|
|