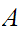 and
and
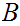 be
Well Ordered then
be
Well Ordered then
12.1 and 12.5 Theorem:
Let
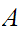 and
and
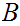 be
Well Ordered then
be
Well Ordered then
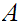 is order isomorphic to a segment of
is order isomorphic to a segment of
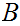 .
.
or
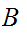 is
order isomorphic to a segment of
is
order isomorphic to a segment of
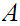 .
.
(For some
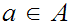 ,
,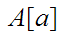 is
order isomorphic to
is
order isomorphic to
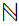 .)
.)
or
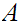 and
and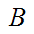 are
order isomorphic.
are
order isomorphic.
(If
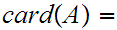 n then
n then
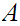 is order isomorphic to
is order isomorphic to
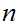 .)
.)
(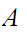 is
order isomorphic to
is
order isomorphic to
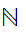 .)
.)
----------------------------------------------------------------------
Another Example.
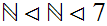 - The Well Ordered Set consisting of the Natural Numbers followed by a copy of
the Natural Numbers followed by
- The Well Ordered Set consisting of the Natural Numbers followed by a copy of
the Natural Numbers followed by
 1,2,3,4,5,6,7
1,2,3,4,5,6,7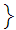
Let
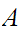 be
Well Ordered then
be
Well Ordered then
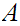 is order isomorphic to a segment of
is order isomorphic to a segment of
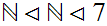 ,or
,or
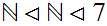 itself.
itself.
or
For some
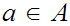 ,
,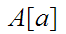 is
order isomorphic to
is
order isomorphic to
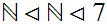 .)
.)
The Axiom of Choice does not play a role in this.
----------------------------------------------------------------------------------
Another Example.
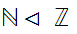 -
The ordered Set consisting of the Natural Numbers followed by the Integers.
-
The ordered Set consisting of the Natural Numbers followed by the Integers.
Consider the following two self-order isomorphisms.
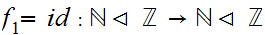
and
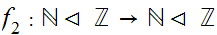
where
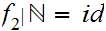 and
and
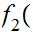 n
n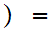 n+1
for n
n+1
for n
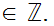
Note that
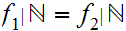 but
but
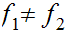 .
.
Consider the structure of the Well Ordered subsets.