Some Tree Arithmetic

Properties of Trees:

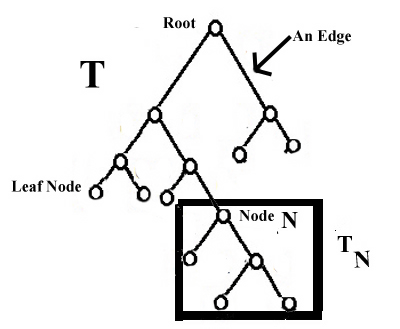
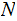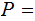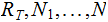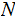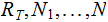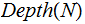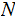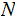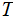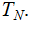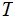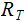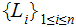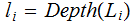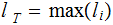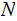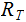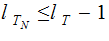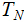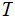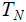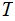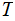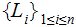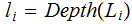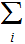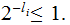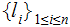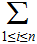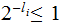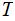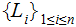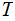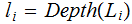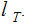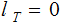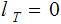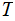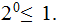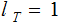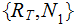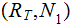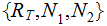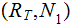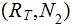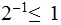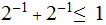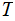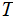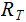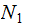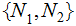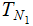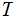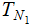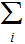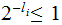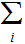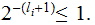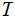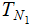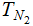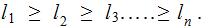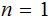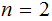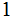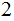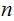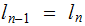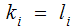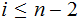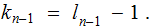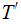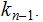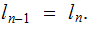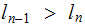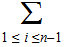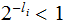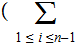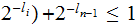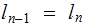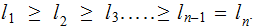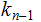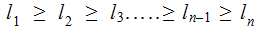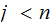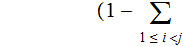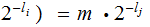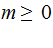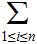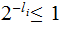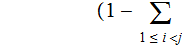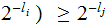• The Components of a Tree are:
  
  

  • Nodes: Can be thought of as places to store data element. Below, We will denote the set of nodes of a Tree 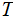as .

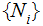  • Edges: Ordered pairs of Nodes. We will use 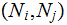as notation for an Edge. The relationship expressed by an Edge is (Parent,Child).

    
    
    

• Properties of Nodes:
  
  

  • Every Tree has a unique Node, called the Root of the Tree that is not the Child of any Parent. We will denote the Root of a Tree as

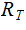
  • Every Child can only have one Parent:

    That is can only be the Child on one Edge.
    
    

  • Parents can have more than one Child,

    That is can be the Parent on more than one Edge.
    
    

  • Common children of a given Parent are called Siblings.
    
    

  • If a Node does not have Children it is called a Leaf.
    
    

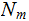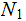  • We call a Descendent of and 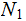an Ancestor of 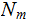if there is a sequence ( "path") of Nodes 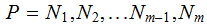and Edges 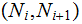for for some .

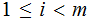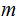• The Defining Property of Trees:
  
  

  • Every Node , other than the Root Node is a Descendent of the Root Node. Moreover the path is unique.

• Additional Properties and Terminology for Trees:
  
  

  • The Depth of a Node is numbers of Ancestors of the Node, computed from the unique path . We use the notation, for the Depth of .

    Note the Depth of the Root is 0 and the Depth of any other Node is the Depth of its Parent +1.
    
    
    
    

  • A Node, , and all its Descendents (and Edges) is a Tree with being the Root. Such a Tree is called a Subtree of the given Tree . We will denote it by

  • If every set of Siblings has a given order then the Tree is called an Ordered Tree.
    
    
    
    

  • If there are at most 2 Siblings for every Parent in an Ordered Tree then the Tree is called Binary.

    
    
    

_________________________________________________________________

Lemma:

Given a Tree with Root , let be the set of its Leaf Nodes and , and let . Finally, let be a Child of then

Proof:

The set of Leaves of is a subset of the set of Leaves of . Moreover any such Leaf, in has Depth 1 less it does in .

________________________________________________________________________

Theorem (Kraft's inequality for Binary Trees):

1. Given a Binary Tree let be the set of its Leaf Nodes and then

2. Conversely, given such that then we can find a Binary Tree and Leaf Nodes of such that .

Proof:

The proof will be by induction on

To prove 1.

The case :

implies that is just the Root Node hence the Lemma amounts to showing

The case :

Since is Binary is either of the form . with a single Edge or . with Edges and .

In the first case we just observe and in the second .

In general:

Since is Binary , has either one Child or two Children .

One Child, the Leaves of are identical to the Leaves of but their Depth with respect to is less so

completing the proof amounts to observing that if then

Two Children, the Leaves of is the disjoint union of the Leaves of and the Leaves of .

Exercise: Finish the arithmetic.

To prove 2.:

By reordering, if necessary, we can assume

The cases and amount to drawing the appropriate or branch tree.

In general, by induction on :

If .

We can find a Tree, , for the list where , and

To complete the proof, just fork the Leaf in corresponding to Each of the two new leaves have Depth

If ,

We have and hence

( Exercise: Why?, a minor variant of a previous argument about Huffman CodesSee Hint below)

The remainder of the proof is a variant of the case . First construct the Tree for

Next fork the leaf for appropriately.

Hint: Show that, in general with and

, some

and since