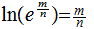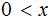 ,
, 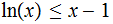 with equality if and only if
with equality if and only if
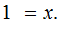
Theorem: For
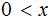 ,
, 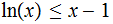 with equality if and only if
with equality if and only if
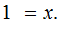
Proof:
For
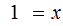 :
:
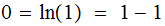
For
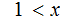 :
:
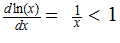
so

and
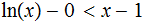
For
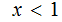 :
:
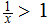
so
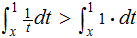
and

Corollary:
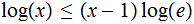 ,
with equality if and only if
,
with equality if and only if
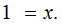
Proof:
Since we will use the notation
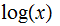 for
for
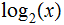 , we will just use that convention although obviously the Corollary is more
general.
, we will just use that convention although obviously the Corollary is more
general.
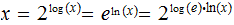
so

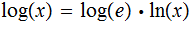
and
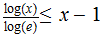
Theorem:
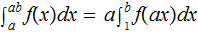
Proof:
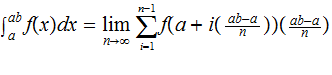



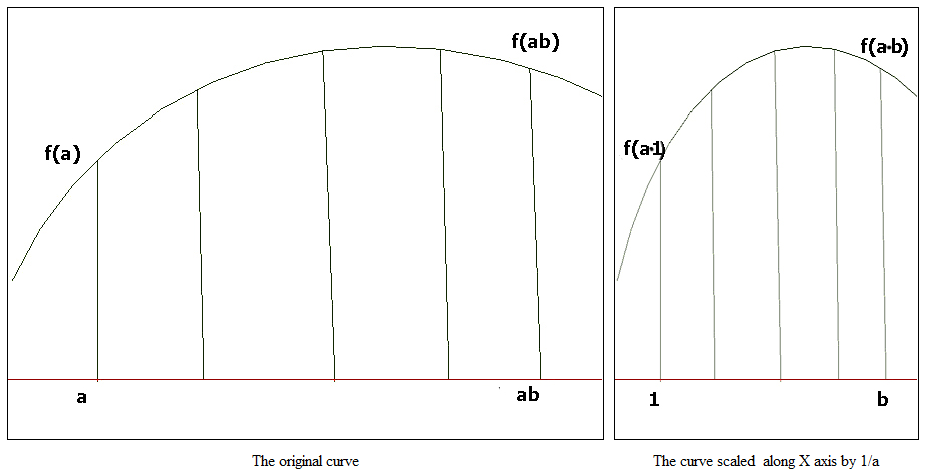
An Alternative Definition:
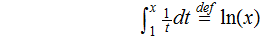
Theorem:
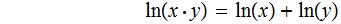
Proof:
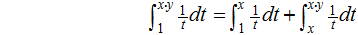



Corollarys:
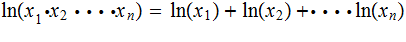
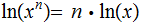
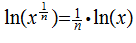
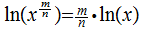
Theorem:
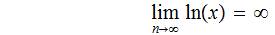
Proof:
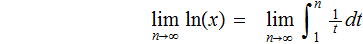
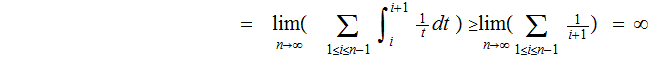
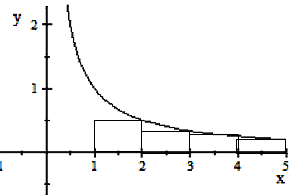
1/2+1/3+1/4+.......
Definition:
 is defined implicitly by the
equation
is defined implicitly by the
equation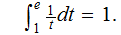
And so: