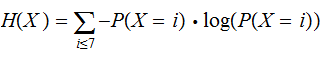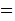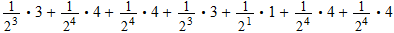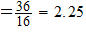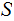 ,
a set of subsets
,
a set of subsets
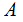 is
called a Sigma Algebra on
is
called a Sigma Algebra on
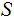 if:
if:
DEFINITION:
Given a set
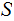 ,
a set of subsets
,
a set of subsets
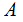 is
called a Sigma Algebra on
is
called a Sigma Algebra on
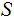 if:
if:
The empty set,
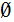
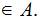
If
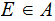 then
then
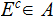 (The complement of
(The complement of
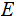 )
)
If
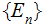 is a countable set of subsets in
is a countable set of subsets in
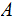 then the union
then the union
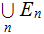 is in
is in
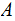 .
.
Some Comments, Terms, and an Example:
When we use the term countable subset we include
finite subsets.
Let
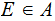 and suppose no subset of
and suppose no subset of
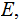 except
except
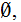 is in
is in
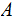 then
then
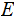 is called an Atom of
is called an Atom of
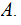
If
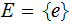 where
where
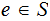 then
then
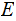 is called a Singleton of
is called a Singleton of
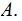 A
Singleton is by definition also an Atom.
A
Singleton is by definition also an Atom.
A Partition of
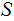 is a set
is a set
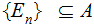 such that
such that
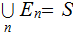 and
and
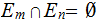 .
.
An Example of a Sigma Algebra: The standard
deck that has two identical Jokers added. A Sigma Algebra
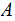 is generated as follows:
is generated as follows:
Each standard card is a Singleton of
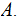
The subset
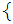 Jo
Jo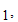 Jo
Jo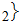 is an Atom of
is an Atom of
The empty set,
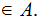
Any union of Singletons and
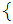 Jo
Jo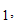 Jo
Jo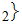 is in
is in
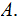
A Simple Example of a Sigma Algebra:
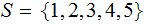

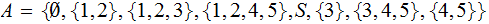
The Atoms? The
Singletons?
Two Properties of Sigma Algebras:
Since
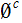
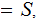
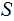
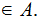
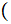
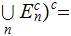

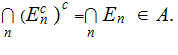
Generating Sigma Algebras:
For any set
 the power set of
the power set of
 P
P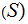 , that is the set of all subsets of
, that is the set of all subsets of
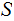 is
a Sigma Algebra.
is
a Sigma Algebra.
Almost by definition.
Let
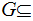 P
P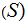 be any collection of subsets of
be any collection of subsets of
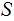 , let
, let
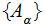 be the set of all Sigma Algebras with
be the set of all Sigma Algebras with
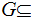
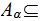 P
P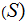
then
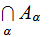 is
a Sigma Algebra called the Sigma Algebra generated by
is
a Sigma Algebra called the Sigma Algebra generated by
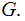 Clearly,
Clearly,
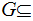
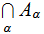 since
since
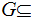
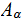 for all
for all
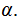
Given a Sigma Algebra
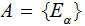 for
a set
for
a set
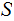 ,a set
,a set
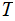 ,
and a function
,
and a function
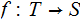 ,
then the collection of subsets
,
then the collection of subsets
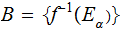 is a Sigma Algebra of
is a Sigma Algebra of
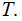
DEFINITION: Suppose we are given a set
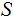 and
and
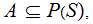 a Sigma Algebra, a Probability Measure on
a Sigma Algebra, a Probability Measure on
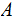 is a function
is a function
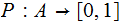 such that
such that
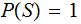
If
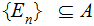 is a countable (again could be finite) subset such that
is a countable (again could be finite) subset such that
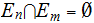 for
for
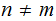 then
then
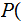
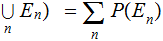
In the context of Probability, we will call
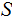 the Sample Space.
the Sample Space.
Let
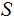 be a finite set and
be a finite set and
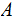 a Sigma Algebra on
a Sigma Algebra on
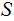 .
For any
.
For any
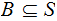 let
let
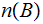 be
the number of members in
be
the number of members in
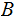 ,
then
,
then
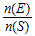 for
all
for
all
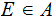 is a Probability Measure on
is a Probability Measure on
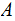 .
.
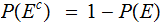 since
since
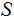
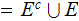 and
and
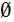
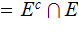
In particular
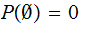 since
since
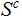
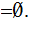
In
general,
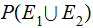
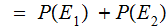
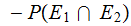
 since
since
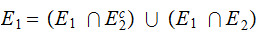 and
and
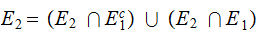
and
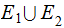
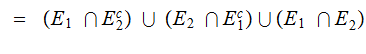
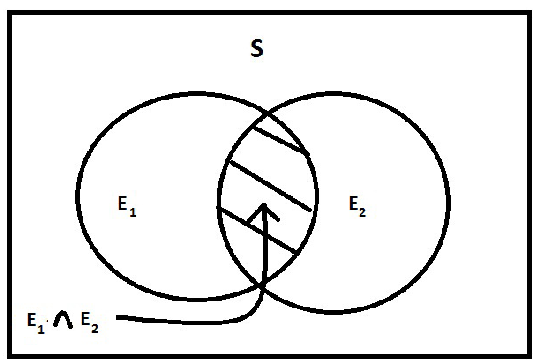
if
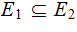 then
then
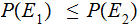 Write
Write
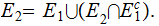
If
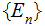 is a Partition of
is a Partition of
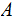 then
then
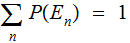 .
.
DEFINITION:
Given a set
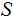 ,
a Sigma Algebra
,
a Sigma Algebra
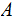 on
on 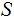 ,
and a countable discrete set
,
and a countable discrete set
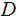 ,
a Discrete Random Variable is a function
,
a Discrete Random Variable is a function
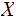
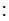
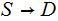 such that if
such that if
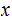 is in the image of
is in the image of
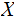 then
then
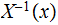 is in
is in
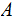 .
.
If
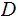 ,
is finite then we will call
,
is finite then we will call
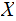 a Finite Random
Variable.
a Finite Random
Variable.
We
write
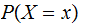 for
for
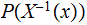
In the setting of 1. , if
 is a Finite Random Variable then
is a Finite Random Variable then
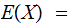
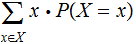
Given a Finite Random Variable
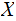
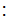
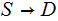 for a Sigma Algebra
for a Sigma Algebra
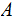 on
on
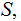 where
where
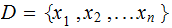 .
And given a Probability Measure
.
And given a Probability Measure
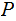 on
on
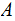 . We will be interested in
. We will be interested in
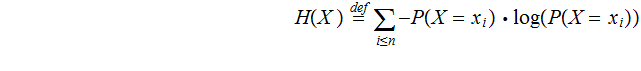
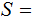 {A,B,C,D,E,F,G} ,
{A,B,C,D,E,F,G} ,
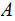 is just the Sigma Algebra of Singletons and, for example
is just the Sigma Algebra of Singletons and, for example
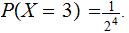
| Singletons | 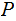 |
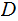 |
| A | 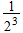 |
1 |
| B | 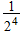 |
2 |
| C | 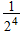 |
3 |
| D | 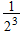 |
4 |
| E | 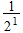 |
5 |
| F | 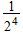 |
6 |
| G | 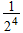 |
7 |