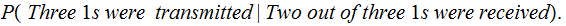 , a Sigma Algebra
, a Sigma Algebra
 ,
a Probability Measure
,
a Probability Measure
 on
on
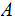 ,
and Events
,
and Events
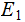 and
and
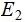 in
in
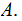 Assuming
Assuming
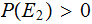
DEFINITION: Given a a Sample Space
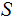 , a Sigma Algebra
, a Sigma Algebra
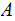 ,
a Probability Measure
,
a Probability Measure
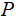 on
on
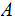 ,
and Events
,
and Events
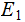 and
and
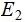 in
in
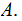 Assuming
Assuming
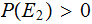
define the Conditional Probability of
 given
given

The Events:
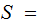 {The days of October and November 2012}
{The days of October and November 2012}
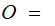 {The days of October 2012}
{The days of October 2012}
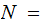 {The days of November 2012}
{The days of November 2012}
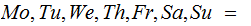 The
various days of the week in
The
various days of the week in
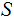
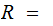 {The days it rained in
{The days it rained in
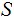 }
}
Finally,
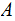 is the Sigma Algebra generated by the given Events.
is the Sigma Algebra generated by the given Events.
The Probabilities:
Most are arithmetic;
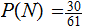 ,
,
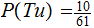 ,
,
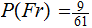 ,
,
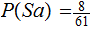
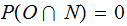
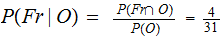 ,
,
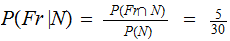
From weather data:
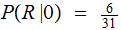 ,
,
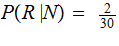
From Calculations:
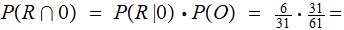
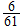
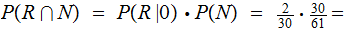
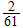
Since
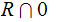 and
and
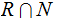
 are
disjoint,
are
disjoint,
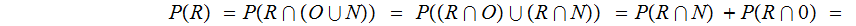
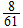
Definition:
Events
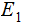 and
and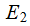 are said to be Independent
if
are said to be Independent
if 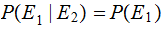 or equivalently
or equivalently
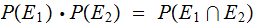 or
equivalently
or
equivalently
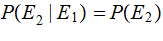
Examples:
The Experiment is flip a coin twice
 is
get a Head the first time and
is
get a Head the first time and
 is
get a Head the second time .
is
get a Head the second time .
The Experiment is choose a card from a standard deck,
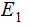 is
the card is a three and
is
the card is a three and
 the
card is a heart.
the
card is a heart.

since
What is the probability that it was a day in October given that we know it
rained on that day?

An Aside: The Rule present above is special case of a more general Bayes Formula of that will come into play later in the semester. I will discuss it at that time but at this point it would be worthwhile to at least review the material in Grinstead and Snell's Introduction to Probability beginning on Page 145.
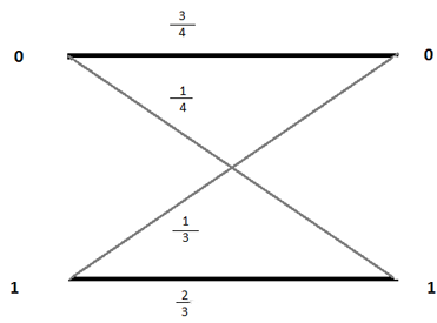
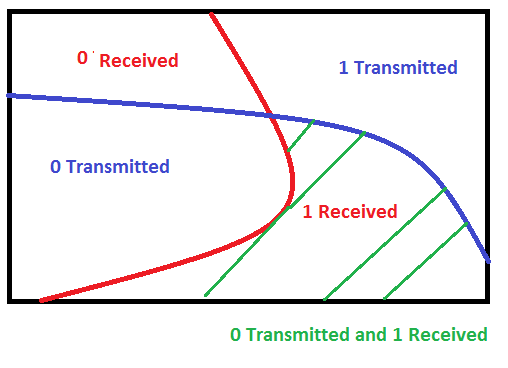
We are given a communications
channel that transmits
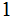 s
and
s
and
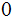 s
with conditional probabilities
s
with conditional probabilities
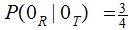 ,
,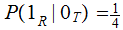 ,
,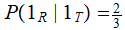 ,
,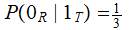 .
.
That is, for example, given that we transmit a
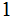 the probability that a
the probability that a
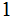 will
be received is
will
be received is
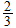 .
.
Question: Assume that we know that
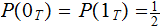 given that we receive a
given that we receive a
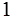 what is the probability that a
what is the probability that a
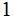 was
transmitted., compute
was
transmitted., compute
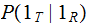 ?
?
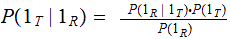
and
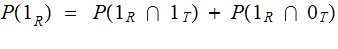

so
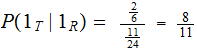
Exercise, The not so wonderful
strategy:
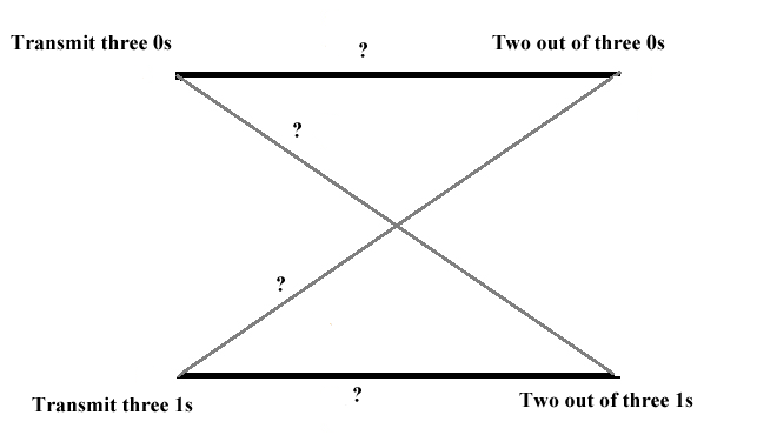
Assume
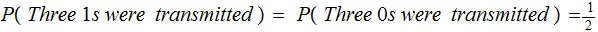 . Fill
in the question marks, using the previous diagram.
. Fill
in the question marks, using the previous diagram.
Finally compute