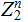 , vectors over the Integers mod 2 . We will be using the
defining property of Linear Transformations
, vectors over the Integers mod 2 . We will be using the
defining property of Linear Transformations
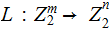 , which
over
, which
over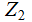 is just:
is just:
In this lecture we will be
working with
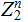 , vectors over the Integers mod 2 . We will be using the
defining property of Linear Transformations
, vectors over the Integers mod 2 . We will be using the
defining property of Linear Transformations
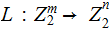 , which
over
, which
over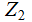 is just:
is just:
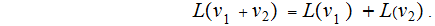
Linear Transformations will be described in Matrix form.
An
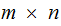 (
(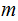 row by
row by
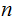 column) matrix will be written as
column) matrix will be written as
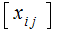 or
or 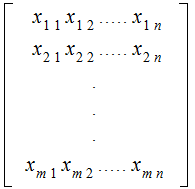 .
We will refer to a
.
We will refer to a
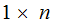 matrix
as an
matrix
as an
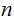 dimensional
row vector and an
dimensional
row vector and an
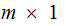 matrix
as an
matrix
as an
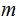 dimensional column vector.
dimensional column vector.
We will sometimes simplify row
vector notation and just write
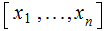 and column vectors notation by writing
and column vectors notation by writing
 leaving
out the trailing or leading 1.
leaving
out the trailing or leading 1.
Given
an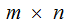 matrix
matrix
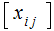 , its transpose
, its transpose
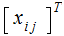 is the
is the
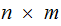 matrix
matrix
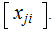
Given
an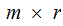 matrix
matrix
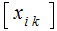 , and an Given
an
, and an Given
an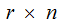 matrix
matrix
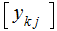 , its product
, its product
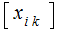
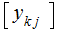 is
the
is
the
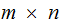 matrix
matrix
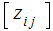 where
where
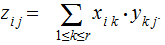
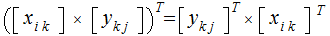
Should the convention be that
our vectors by row vectors and the corresponding Linear Transformation be
matrix multiplication on the right or should they be column vectors and matrix
multiplication be on the left?
Answer: it does not matter as long as we are consistant.
Warning: As you search the literature, including the Web, make sure you note which convention is being used.
Our Convention:
Unless noted, vectors will be row vectors with multiplication on the right.
Definition:
Suppose we are given alphabet of symbols
 and
an encoding
and
an encoding
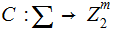 then is called a Linear Code if
then is called a Linear Code if
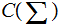 is
a subspace of
is
a subspace of
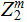 .
.
7 bit ASCII is a Linear Code since every vector in
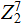 is a code word.
is a code word.
If
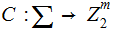 is a Linear Code and
is a Linear Code and
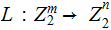 is a 1 to 1 Linear Transformation then
is a 1 to 1 Linear Transformation then
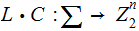 is a Linear Code.
is a Linear Code.
Given a Linear Code
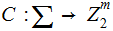
We are given a 1 to 1 Linear Transformation
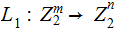 in
the form of a Matrix
in
the form of a Matrix
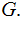
We are also given a Linear Transformation ,not 1 to 1,
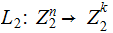 in
the form of a Matrix
in
the form of a Matrix
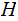
Methodology:
Given a symbol
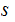 encode
it as
encode
it as
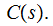 Next encode
Next encode
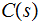 for transmission as
for transmission as
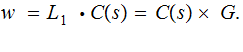
Transmit
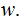 Denote the vector that is received by
Denote the vector that is received by
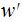 . Maybe
. Maybe
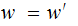 maybe
not.
maybe
not.
Compute
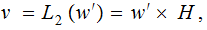 below if
below if
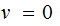 success,
if not a transmission error.
success,
if not a transmission error.
To make the notation a bit simpler will work with "mini-ASCII", some 4 bit
encoding
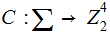 where every vector is a code word.
where every vector is a code word.
We use the matricies:
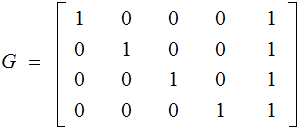 and
and
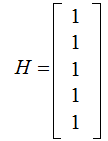
for Even Parity checking., we
use
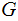 to
encode 4 bit words as 5 bit words for
transmission and
to
encode 4 bit words as 5 bit words for
transmission and
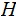 to check for errors at the receiving end.
to check for errors at the receiving end.
Given
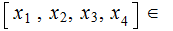
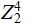
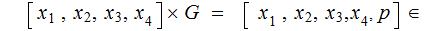
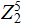
Note that
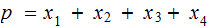 is an Even Parity bit.
is an Even Parity bit.
We transmit
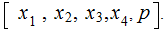 At the receiving end
compute
At the receiving end
compute 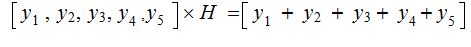
Assuming there is at most one bit error:
If the
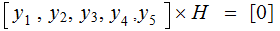 the
transmission was without error
the
transmission was without error
If
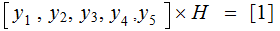 there
was a transmission error.
there
was a transmission error.
Question: Even Parity Check is a Linear Code, is Odd Parity Check?
 Hamming Code :
Hamming Code :
The matricies:
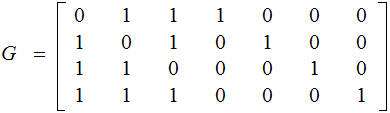 and
and
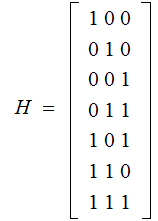
Again, given
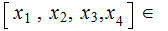
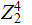 we
encode it by multiplying on the right by
we
encode it by multiplying on the right by
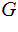
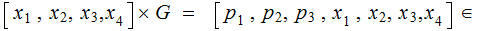
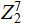
An Aside: Having the Identity submatrix as the last four
column vectors of
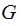 seems
to be somewhat of a standard so I am following that convention.
seems
to be somewhat of a standard so I am following that convention.
 Hamming Code:
Hamming Code:
Since
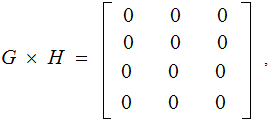 if
if
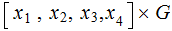 is correctly received
is correctly received
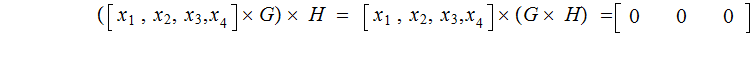
Writing
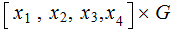 as
as
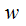 suppose
there is a single bit transmission error:
suppose
there is a single bit transmission error:
The
vector received is of the form
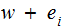 where
where
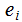
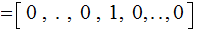 ,
,
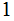 in
the
in
the 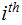 position
position
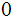 in every other position.
in every other position.
(Flipping a bit is, in effect, just adding an appropriate unit vector)
Since
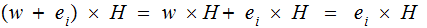 ,
which is just the
,
which is just the
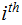 row of
row of
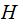 ,
the
,
the
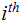 bit
is an error.
bit
is an error.