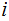 and
and
 a Sigma Algebra on
a Sigma Algebra on
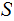 ,
and a Probability Measure
,
and a Probability Measure
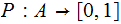
As the title implies, Shannon's definition of
Information, below, is focused on communication
(of data), in particular topics such as data compression and error detection
and correction. We will want to understand the "mathematical meaning" of this
statement however some informal understanding of that he was looking at may be
useful.
I want to communicate class readings to you. We agree that 0 represents Raza's text and 1 represents MacKay's. I send you the message
1-87. You know that you need to be looking at Page
87 of MacKay. How did you know that I just did not flip
87 Heads? Answer, both ends of the communication channel
agree on "meaning" or the "content." of messages.
The smallest element of computer storage. For our purposes, a
single binary digit (0 or 1) and , assuming
the Bit's in a giving computer's memory are are randomly distributed, when I
learn the value of a single Bit then I have learned 1 Bit of
Information.
Definition:
We are given a set
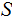 and
and
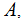 a Sigma Algebra on
a Sigma Algebra on
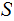 ,
and a Probability Measure
,
and a Probability Measure
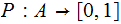
Let
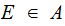 be
an event such that
be
an event such that
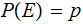 .
We define
.
We define

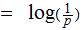
We say that we have learned
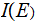 bit's
of Information when we learned that
bit's
of Information when we learned that
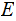 has occured.
has occured.
1. If an event
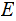 occurs with probability
occurs with probability
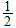 then
then
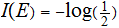
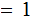 .
.
2. If an event
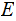 occurs with probability
occurs with probability
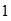 then
then
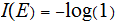
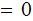 ,
we have learned nothing.
,
we have learned nothing.
3. If an event
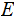 occurs with probability
occurs with probability
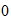 then
then
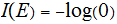
 ?.
?.
Mathematically, if we have events
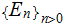 and
and
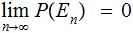 then
then 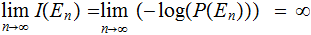 .
.
Definition (Provisional):
Given a set
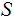 and
and
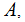 a Sigma Algebra on
a Sigma Algebra on
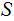 ,
,
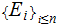 a Partition of
a Partition of
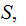 and
a Probability Measure
and
a Probability Measure
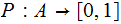 with
with
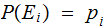
Define:
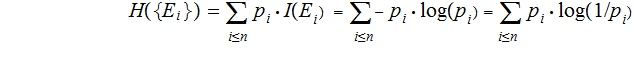
Given:
A set
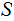 and
and
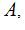 a Sigma Algebra on
a Sigma Algebra on
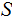 ,
,
A Finite Random Variable
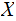 on
on
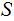 , taking values
, taking values
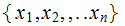 and
such that
and
such that
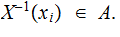
A Probability Measure
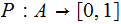
Define The Entropy of
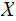 :
:
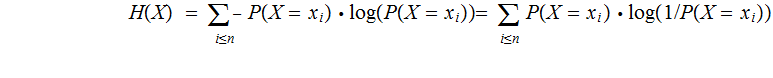
We say that we have learned
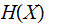 bits
on Information when we learn the outcome of experiment
bits
on Information when we learn the outcome of experiment
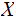 .
.
The reason for the Provisional Definition is that the Entropy has nothing to
do with the actual values
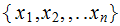 only with the Partition
only with the Partition
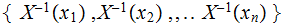 .
.
(See the comments in The Paper above ). A more
dramatic example, though maybe less relevent, would be two different
experiments.
A coin is tossed, if it is a Head you win a penny, if it is a Tail I win a
penny.
A coin is tossed, if it is a Head you win $1000, if it is a Tail I win a
penny.
How many bits of Information do I get when I learn the outcome? For 1.? For 2.?
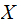 is
a constant function
is
a constant function
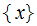 ,
so
,
so
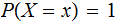 and
and
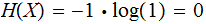 .
There is no uncertainty as to the outcome of the experiment, we learn nothing
when we learn the result.
.
There is no uncertainty as to the outcome of the experiment, we learn nothing
when we learn the result.
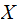 takes two values
takes two values
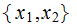 and
and
The two possible outcomes, each have probability
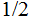 :
:
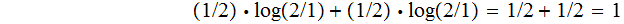 ,
we expect to learn
,
we expect to learn
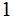 bit of Information.
bit of Information.
The two possible outcomes have probability
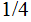 and
the other with probability
and
the other with probability
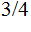
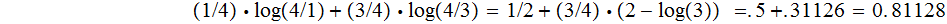
We expect to learn less than
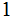 bit of Information because there is less uncertainty.
bit of Information because there is less uncertainty.
Writing the two probabilities as
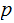 and
and
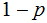 and
and
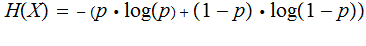
Theorem:

( As
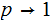 the outcome of the experiment becomes more and more certain so, intuitively,
we expect
the outcome of the experiment becomes more and more certain so, intuitively,
we expect
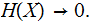 )
)
Proof:
Again
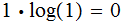 so, for the moment writing
so, for the moment writing
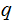 for
for
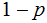 we need only to look at
we need only to look at
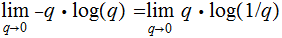 which is an indeterminate form of type
which is an indeterminate form of type
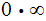 .
.
Rewriting the limit as
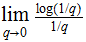 we have an indeterminate form of type
we have an indeterminate form of type
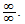
Applying L'Hospital's Rule. we have
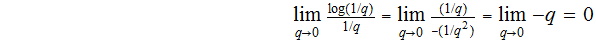
One has a bag containing a red, blue, and green ball. A ball is picked at
random, how much Information is obtained? Since any ball selection is assumed
equiprobable:
The Problem:
You are given 12 numbered balls that otherwise look identical in all respects except one of them has a different weight. It could be lighter or heavier.
You are given a balance and you can use that balance, and only that balance, to weight any number of ball against any other number.
Find out which is the ball of different weight and whether it is lighter or heavier.
Shannon's Clue:
There are 24 possible, we assume equiprobable, outcomes
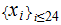 ,
. which ball is of different weight and is it heavier or lighter, in
particular
,
. which ball is of different weight and is it heavier or lighter, in
particular
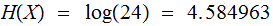 .
.
If we could come up with a way of getting a slightly more than
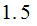 bits
of information with each weighing experiment we should be able to do it with 3
weighings.
bits
of information with each weighing experiment we should be able to do it with 3
weighings.
Exercise: Come up with a strategy. (Do not watch MacKay's second lecture for a bit it will spoil the fun).
Assignment( Due February 14): Suppose you had 6 numbered balls as above. What does Shannon say? Find a weighing strategy.
In the setting of the Definition of Entropy:
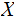 takes values
takes values
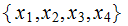 and
and
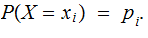
The two pictures:
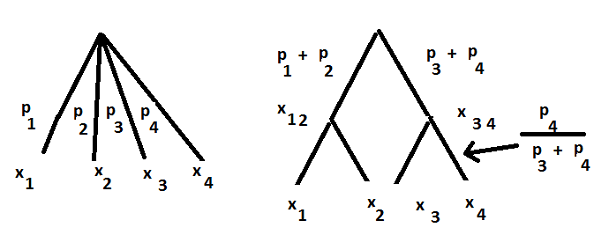
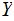 takes values
takes values
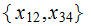 and
and
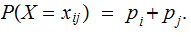
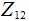 takes values
takes values
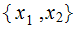 and
and
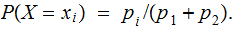
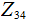 takes values
takes values
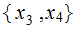 and
and
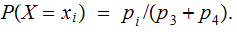
The Formula:
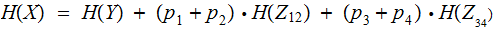
The Proof by Addition:
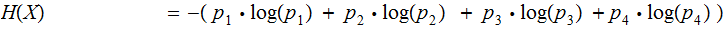
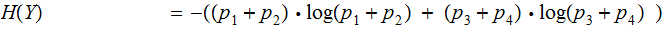
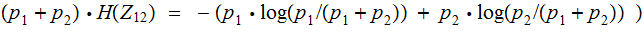
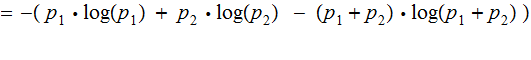
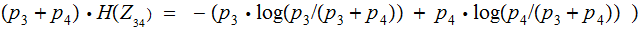
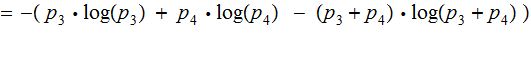
Example:
I flip a coin twice. I tell you the outcome in two stages. First I tell you the outcome of the first flip and then the outcome of the second.
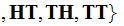 ,
,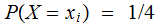 and
and
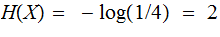
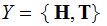 ,
,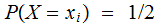 and
and
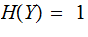
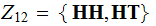 ,
,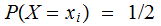 ,
,
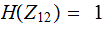 and
and
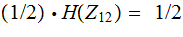
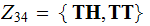 ,
,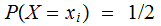 ,
,
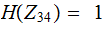 and
and
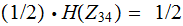
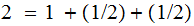
Exercise (Due February 14):
I choose a ball at random from a bag containing 3 red balls and 1 blue ball and I choose a card at random from an ordinary deck of playing cards. If I choose a red ball I tell you the cards rank (A,2,3....,K).
If I chose the blue ball I tell you the cards suit (S,H,D,C).
How bits of Information do you expect to get by learning the result of my experiment?
Verify that the Partition Formula produces the correct result for this experiment.
In the previous material on Bernoulli Trials we computed:
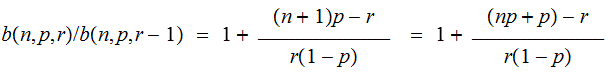
Suppose
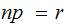 is
an integer.
is
an integer.
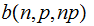 is
a maximum since:
is
a maximum since:
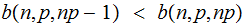 and
and
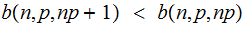
We have the following:
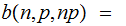
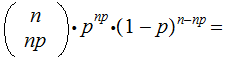
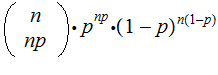
Since
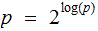 and
and
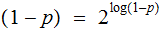

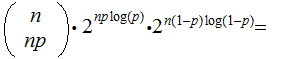
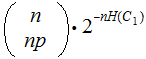
Suppose
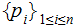 and
and
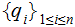 are two probablility distributions, then
are two probablility distributions, then
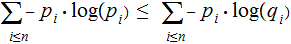
with equality if and only if
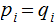 for
for
Proof:
Since
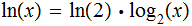 and
and
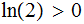 proving theTheorem is equivalent to proving
proving theTheorem is equivalent to proving
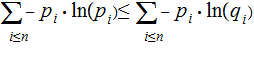
Assume for the moment that all
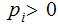 and
and
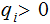 , since
, since
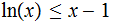 for
for
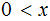 , we have
, we have
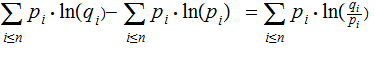
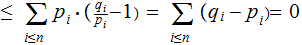
but
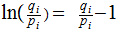 only
if
only
if
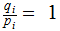
The case where some
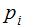 or
or
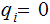 is fairly straight forward and similiar to previous calculations involving "
is fairly straight forward and similiar to previous calculations involving "
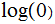 ".
".
Corollary: Given
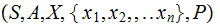 as
above
as
above
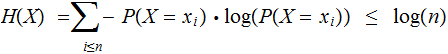
In particular if
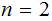
 then
then
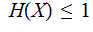
Proof:
Letting
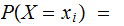
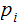 and
and 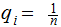 for all
for all