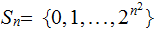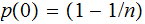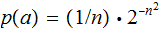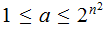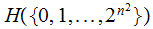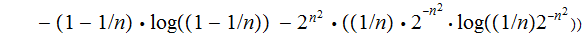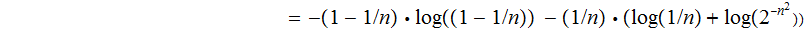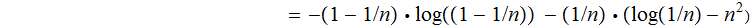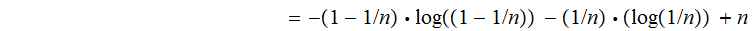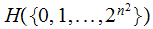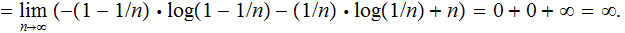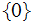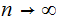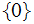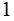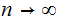An Interesting Calculation
Of course at this point
it is questionable what is meant by a measure of uncertainty. The
clarification of this concept has to come gradually; it is, in essence, the
central theme of information theory. The problem can be approached in either
of two, not necessarily exclusive, ways:
-
First postulate the desired properties of such an uncertainty measure;
then derive the functional form of
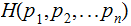 .
The postulation of the desired properties can be based on some intuitive
approach such as physical motivation or "usefulness" for some purpose, but
after such a postulate is adopted, mathematical discipline must prevail and no
further intuitive approach may be employed.
.
The postulation of the desired properties can be based on some intuitive
approach such as physical motivation or "usefulness" for some purpose, but
after such a postulate is adopted, mathematical discipline must prevail and no
further intuitive approach may be employed.
-
Assume a known functional
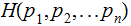 associated
with a finite probability schem and justify its "usefulness" for the physical
problems under consideration.
associated
with a finite probability schem and justify its "usefulness" for the physical
problems under consideration.
An Introduction to Information Theory
Fazolollah M. Reze
____________________________________________________________________________________________________________________________
Setting aside some of the formalities, let
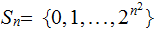 ,
,
 ,
with probability distribution
,
with probability distribution

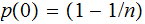 and
and
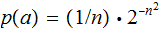 for
for
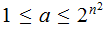
We are just thinking of the numbers as the possible events and the experiment
is, write the numbers on separate pieces of papers and draw one from
a hat.
The Entropy
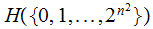 is:
is:
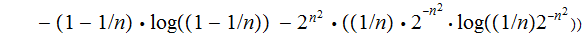
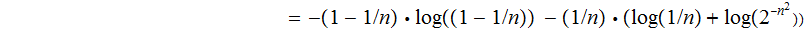
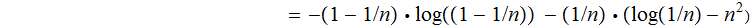
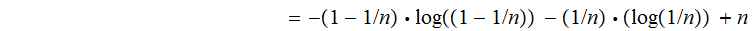
Hence:

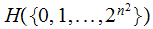
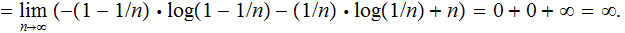
___________________________________________________________________________________________________
Analysis:
We have a series of experiments, each with, amongst other possible outcomes,
outcome
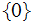 .
.
Restated, although the probabilistic outcome of the sequence of experiments
becomes more and more certain, learning the outcome of each succeeding
experiment produces more and more "Shannon Information."
The Question: Why?
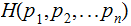 .
The postulation of the desired properties can be based on some intuitive
approach such as physical motivation or "usefulness" for some purpose, but
after such a postulate is adopted, mathematical discipline must prevail and no
further intuitive approach may be employed.
.
The postulation of the desired properties can be based on some intuitive
approach such as physical motivation or "usefulness" for some purpose, but
after such a postulate is adopted, mathematical discipline must prevail and no
further intuitive approach may be employed.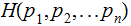 associated
with a finite probability schem and justify its "usefulness" for the physical
problems under consideration.
associated
with a finite probability schem and justify its "usefulness" for the physical
problems under consideration.