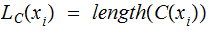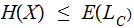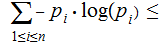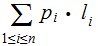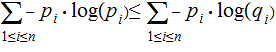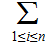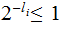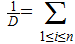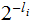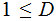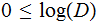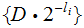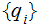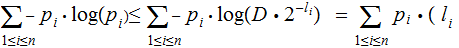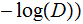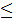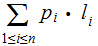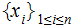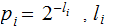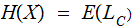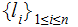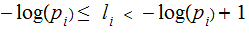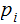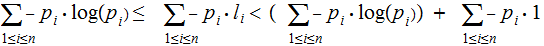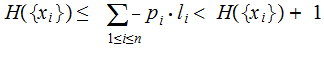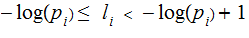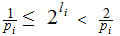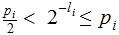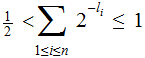Shannon's Noiseless Coding Theorem
Assumptions:
___________________________________________________________________________________________________
Theorem:
Under the above assumptions, for any such
:
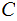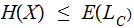
In particular,
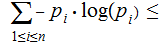
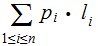
The average length of an encoded symbol is greater than or equal to the
Entropy.
___________________________________________________________________________________________________
Proof:
Recall Gibb's Inequality:
If
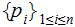and
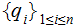are two probablility distributions, then
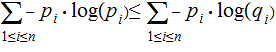
And Kraft's
inequality:
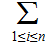
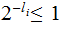
Define
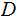by the formula:
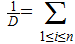
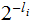
By Kraft's inequality we have
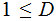thus
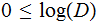
Letting
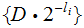be the probability distribution
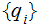we have:
_____________________________________________________________________________________________________________
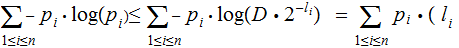
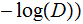
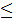
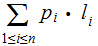
Realizing the Bound (Huffman Code for Certain
Probability Measures):
Theorem:
Given
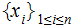as above with
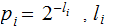then
the associated Huffman Code, satisifies the equation
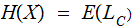
, the expect length of codes is the Entropy of the symbol set.
Proof:
A
previous discussion.
_____________________________________________________________________________________________________________
Approximating the Bound (Shannon-Fano Coding):
The following approximation to the Shannon Noiseless coding bound is less
efficient than Huffman's proceedure but is a bit easier to demonstrate.
In the setting above, just choose integers
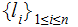such
that:
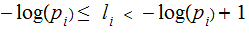
Suppose we knew that we could find an instantanous code with these lengths,
then, multiplying each inequality by the appropriate
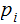and
then adding them we get
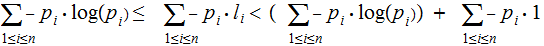
or
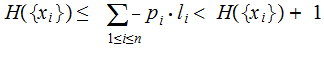
To show that we can find such a code:
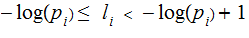
can be rewritten as:
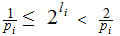and
by inverting the terms
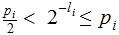
again by adding the inequalities we get:
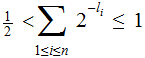
Which, again using Kraft's inequality, says that such an instantanous code
exists:
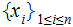with probability distribution
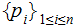We refer to
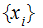as
the set of symbols . We are interested on the Sigma Algebra
and Probability Measure generated by
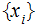and
,
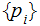
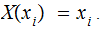
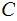again, each symbol is coded as a string on 1 s and 0
s and no code string in the prefix of another. We wish to consider a
second Random Variable
