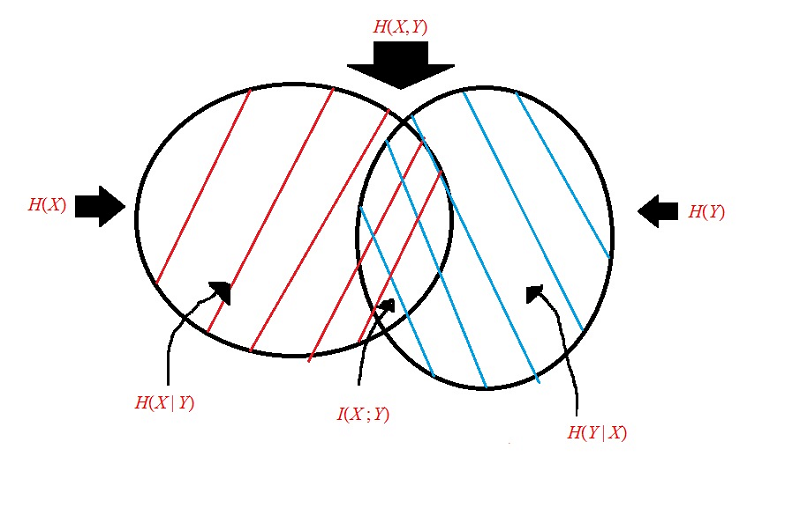

 ,
the expected Joint Information in
,
the expected Joint Information in
 and
and
 The Information in
The Information in
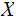 or in
or in
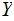
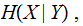 the
red thatched area minus the blue, the expected Information left in
the
red thatched area minus the blue, the expected Information left in
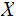 after
we learn about
after
we learn about
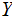 .
.
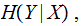 the
blue thatched area minus the red, the expected Information left in
the
blue thatched area minus the red, the expected Information left in
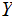 after we learn about
after we learn about
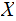 .
.
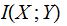 is
the expected Mutual, Information in
is
the expected Mutual, Information in
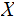 and
and
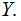 If I have Information about
If I have Information about
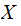 then I also have some Information about
then I also have some Information about
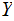
.
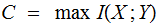 :
Given a Channel , by modifying
:
Given a Channel , by modifying
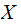 s
distribution, how big can I make the relative overlap, the shared Information.
s
distribution, how big can I make the relative overlap, the shared Information.