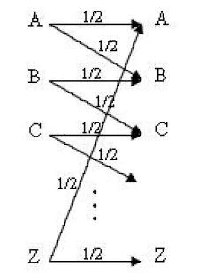
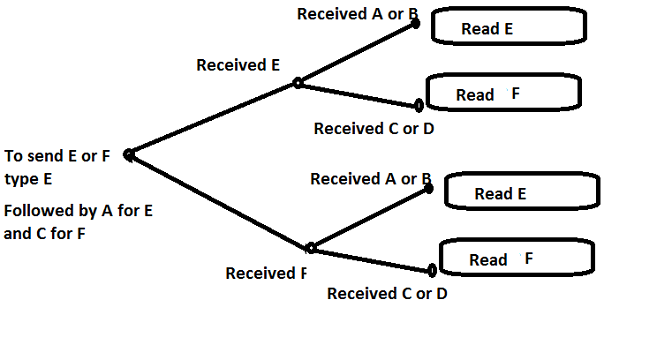
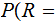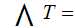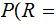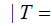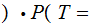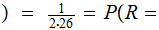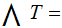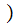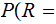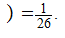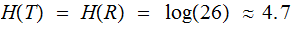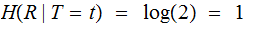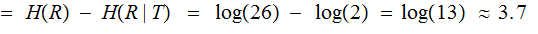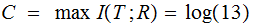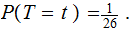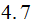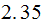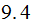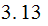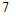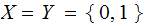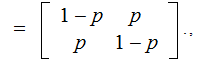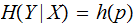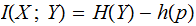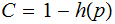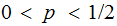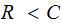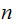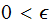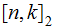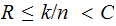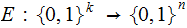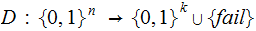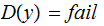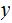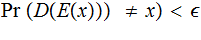A typewriter with only 26 keys {A,B,..,Z} no shift
key, in particular, the input and output alphabets are
{A,B,..,Z}
The typewriter is defective in that if you strike a key with a given letter, that letter or the letter following will be printed with equal probability.
For an A you get an
A or a B. To complete
the cycle, for a Z you get a
Z or an A. For
example
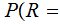 E
E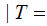 E
E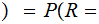 F
F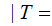 E
E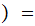
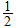
Finally, to simplify our calculations we assume a Uniform Distribution
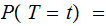
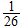 for
any letter
for
any letter