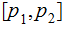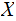
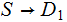 and
and
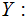
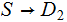 for the same Sample Space
for the same Sample Space
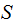 and
Sigma Algebra
and
Sigma Algebra
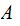 on
on
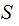 are called jointly distributed.
are called jointly distributed.
Definition: Two Random Variables
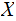
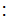
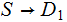 and
and
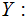
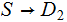 for the same Sample Space
for the same Sample Space
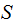 and
Sigma Algebra
and
Sigma Algebra
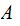 on
on
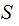 are called jointly distributed.
are called jointly distributed.
Notes:
We assume we are given , a Sample Space
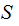 ,
Sigma Algebra
,
Sigma Algebra
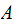 on
on
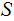 , and Probability Measure
, and Probability Measure
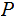 on
on
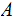 .
.
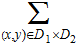
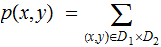
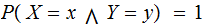
We will simplify the notation a bit by using the notation
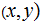 for
for
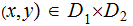 ,
,
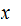 for
for
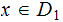 ,and
,and
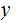 for
for
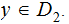
However we need to be careful with this notation. In particular,
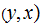 would
be the simplified notation for
would
be the simplified notation for
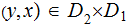
See the definition immediately below.
Definitions:
The Joint Entropy
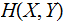 of a pair of Finite Random Variables
of a pair of Finite Random Variables
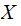 and
and
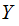 on
on
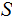 is
defined as:
is
defined as:
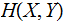
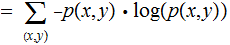
Note that.
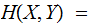
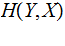
For each
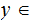
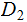 , we have the Conditional Entropy
of
, we have the Conditional Entropy
of 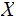 given
given
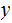 ,
,
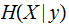
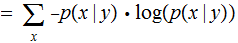
Finally The Conditional Entropy
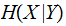 of a pair of Finite Random Variables
of a pair of Finite Random Variables
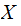 and
and
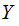 is defined as follows:
is defined as follows:
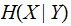
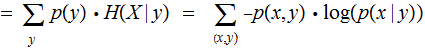
Reversing the roles of
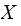 and
and
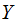 for each
for each
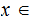
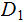 we have:
we have:
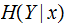
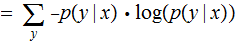
and
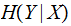
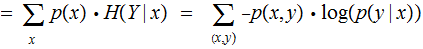
For
 Read:
Having learned the value
Read:
Having learned the value
 has
take
has
take
 is the Information you get when you learn the value
is the Information you get when you learn the value
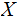 has
taken
has
taken
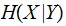 is the Expected Value of
is the Expected Value of
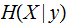
Theorem:
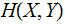
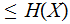
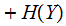

with equality if and only
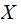 and
and
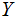 are
independent, that is
are
independent, that is
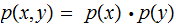 for all
for all
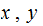 .
.
Proof:
By Gibb's inequality, with
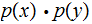 playing the role of the
playing the role of the
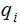 's for the pairs
's for the pairs
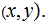
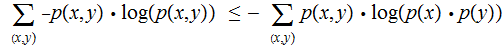
With equality if and only if
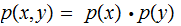 and
thus
and
thus
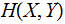
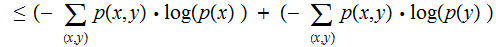
and,
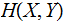
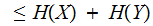
since,
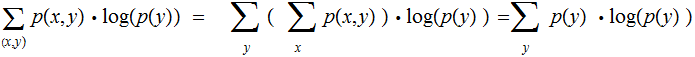
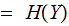
similarly for
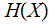
Theorem
(The Chain Rule):
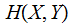
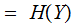
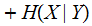 equivalently
equivalently
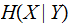
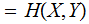
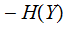
The Information you receive when you learn
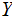 plus the Information you receive when you learn about
plus the Information you receive when you learn about
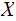 given you know
given you know
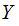
equals the Information you receive what you learn when you learn about both
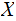 and
and
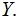
The Information you receive when you learn about both
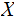 and
and
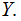 minus the Information you receive when you learn about
minus the Information you receive when you learn about
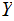

equals the Information you receive when you learn about about
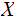 given you know
given you know

Proof (the second version):
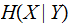
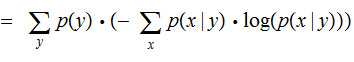
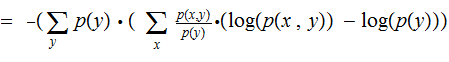
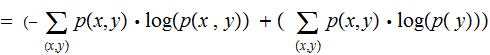
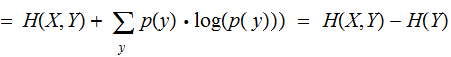
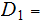
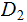 and
and
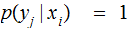 ,
,
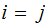
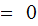 ,
,
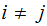
No Noise,
 and thus
and thus
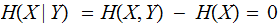
We learn nothing new when we know what character was received given that we know what was transmitted.
since
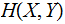
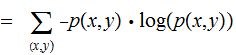
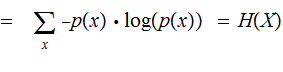
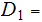
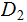 and
and
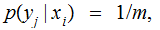 all
all
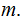
All Noise,
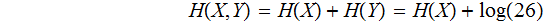 and
and
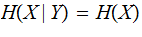
 since
the Random Variables are independent.
since
the Random Variables are independent.
Exercise ( Due March 5): Compute
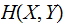 and
and
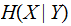 for a Binary Symmetric Channel and input vector
for a Binary Symmetric Channel and input vector