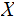
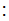
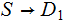 and
and
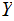
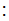
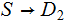 their Mutual Information is defined as follows:
their Mutual Information is defined as follows:
Definition:
In the setting of the previous lecture, given two jointly distributed Finite
Random Variables
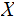
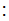
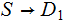 and
and
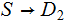 their Mutual Information is defined as follows:
their Mutual Information is defined as follows:
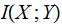
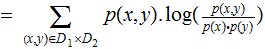
There is no minus sign!
If
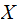 and
and
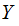 are
Independent
are
Independent
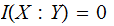 since
since
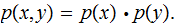 There
is no Mutual Information, Example 2 from the previous section.
There
is no Mutual Information, Example 2 from the previous section.
For a noiseless Channel
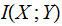
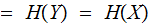
Since
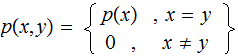
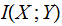
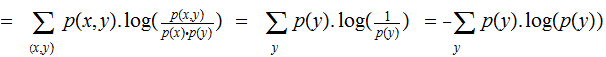
and essentially the same calculation for
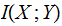
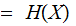 .
All Information is Mutual.
.
All Information is Mutual.
Theorem:
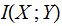
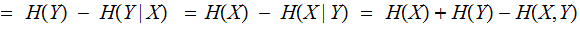
Proofs:
These are all simple variants of the definition, the calculation in the second
bullet above and the material in the previous lecture. For example,
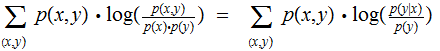
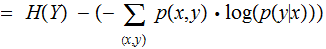
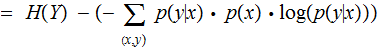
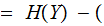
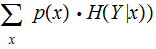
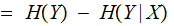
One might read
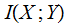 , the Mutual Information as:
, the Mutual Information as:
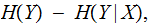 the
average information about the character
received
the
average information about the character
received after
the transmission noise has been removed.
after
the transmission noise has been removed.
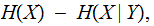 the
average information about the character
sent
the
average information about the character
sent after
the Bayesian noise has been removed.
after
the Bayesian noise has been removed.
The information in
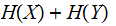 after
a copy of the joint information has been removed, the Mutual Information
getting counted twice
after
a copy of the joint information has been removed, the Mutual Information
getting counted twice
We have Random Variables
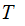 and
and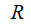 and
and
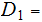
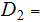 {A,B,..,Z}
{A,B,..,Z}
The two special cases to be considered are :
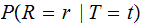
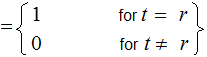 , error free transmission.
, error free transmission.
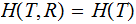 and
and
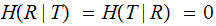
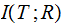
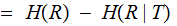
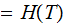 , All of the information is in what is transmitted.
, All of the information is in what is transmitted.
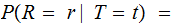
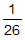 for all
for all
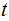 and
and
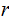 ,
total noise
,
total noise
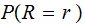
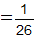 ,
,
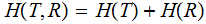 ,
,
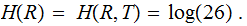
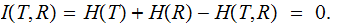 Since
Since
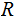 and
and
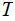 are independent.there is no mutual information.
are independent.there is no mutual information.
Definition:
 for
a given
channel
for
a given
channel 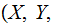
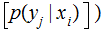 ,
the Channel Capacity,
,
the Channel Capacity,
 is
defined by the formula
is
defined by the formula
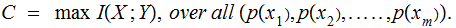
For the example of a Binary Symmetric Channel, since
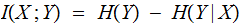 and
and
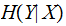 is
constant. The maximum is achieved when
is
constant. The maximum is achieved when
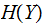 is
a maximum (see below)
is
a maximum (see below)
Exercise (Due March 7) : Compute the Channel
Capacity for a Binary Symmetric Channel in terms of
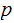 ?
?
Theorem:
If the values of each row of a Channel Matrix ,
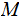 , are a permutation of the values in any other row then
, are a permutation of the values in any other row then
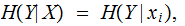 for
any
for
any
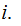 In
particular
In
particular
if a Channel is Symmetric then
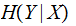 is
independent of the input probability vector
is
independent of the input probability vector
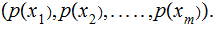
If the values of each column of a Channel Matrix ,
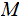 , are a permutation of the values in any other column then
, are a permutation of the values in any other column then
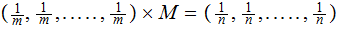
If a Channel is Symmetric:
The
Channel Capacity
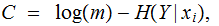 for
any
for
any
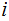
.
Since
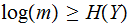 for
any
for
any
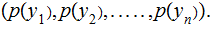
Proof:
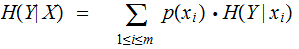 and
and
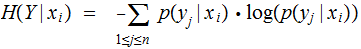 but the rows of the channel matrix all have the same values, again the order
may be different
but the rows of the channel matrix all have the same values, again the order
may be different
so
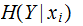 is
independent of
is
independent of
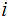 .
In particular,
.
In particular,
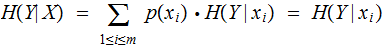 for
any
for
any
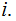
For a given
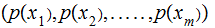 ,
,
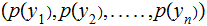
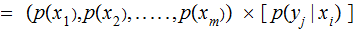 in
particular since the columns all have the same values
in
particular since the columns all have the same values
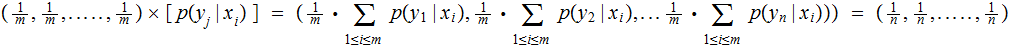
since
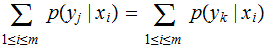 any
any
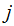 and
and
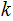 ,and
,and
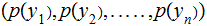 is
a probability distribution.
is
a probability distribution.
