Huffman Coding - Lossless Data Compression
Very Early Data Compression:
The Morse Code and the
Telegraph:
was developed in the 1830s and 1840s and used electric pulses sent down
a wire to control a "receiver" electromagnet. There were three basic
signals, a short pulse or dot, a long pulse or dash and "pause" for spacing.
Different length pauses represented different separators. A characteristic of
Morse Code is that, to some extent, common letters use shorter sequences of dots
and dashes.
A major milestone in global communication
was the transatlantic telegraph
cable project began in 1857. It was not effectively
completed and put into service until July 28, 1866. however On August 16, 1858
President James Buchanan and Queen Victoria did exchange messages across the
Atlantic.


Presidents
Lincoln and Obama in their respective Situation Rooms monotoring developments,
using modern technology.
The image of President Lincoln is
from the new movie, "Lincoln."
(See pages: 183-185 , Reza: An Introduction to Information
Theory)
_________________________________________________________________________________________________________________________________
Class Note Regarding Information Redundancy in English
R*pl*c* v*w*ls w*th g*n*r*c symb*ls.
_________________________________________________________________________________________________________________________________
Huffman Coding
MacKay's Lecture 4 "How to Compress a Redundant File"
Assumptions:
- The data can be transmitted without
error.
- We are going to use strings of 1's and
0's to encode symbols to transmit code.
- We can use variable length strings to encode symbols but we want
the code to be Prefix free in the sense that no code string in
the prefix of another. In the literature this is just called a Prefix
Code.
- Given an "alphabet" of symbols and their probabilities of being
transmitted, We want the code to be efficient in the sense that the expected length of
transmitted strings will be the shortest.
David Huffman
gave a "best possible" algorithm for
doing this. The algorithm for generating a Huffman tree is very simple and for
the moment we will just present one, hopefully sufficiently general,
example.
The Process:
We begin with a table of symbols and their
probabilities. The given probabilities are just suggestive.
| Symbol |
Probability |
| A |
5 / 21 |
| B |
2 / 21 |
| C |
1 / 21 |
| D |
2 / 21 |
| E |
7 / 21 |
| F |
1 / 21 |
| G |
2 / 21 |
| H |
1 /
21 |
Next, dropping the "redundant '
/21'" and replacing "Probability" with "Frequency," we rearrange the list so
that the Symbol's with the lowest Frequency are at the bottom. Of
course, this step may not have a unique result.
| Symbol |
Frequency |
| E |
7 |
| A |
5 |
| B |
2 |
| D |
2 |
| G |
2 |
| C |
1 |
| F |
1 |
| H |
1
|
Next, starting at the bottom,
with two symbols of least frequency we combine them (considering the result a
single character) and, if necessary rearrange, the table.
| Symbol |
Frequency |
| E |
7 |
| A |
5 |
| B |
2 |
| D |
2 |
| G |
2 |
| [F,H] |
2 |
| C |
1
|
Repeating this process
until we have a single row we get.
| Symbol |
Frequency
|
| E |
7 |
| A |
5 |
| [[F,H],[C]] |
3 |
| B |
2 |
| D |
2 |
| G |
2
|
|
---> |
| Symbol |
Frequency
|
| E |
7 |
| A |
5 |
| [D,G] |
4 |
| [[F,H],C] |
3 |
| B |
2
|
|
---> |
| Symbol |
Frequency
|
| E |
7 |
| A |
5 |
| [[[F,H],C],B] |
5 |
| [D,G] |
4
|
|
---> |
| Symbol |
Frequency
|
| [[[[F,H],C],B],[D,G]] |
9 |
| E |
7 |
| A |
5
|
|
---> |
|
And finally for the purposes of
this example we get (If we were being very formal, we would go a step further).
| Symbol |
Frequency |
| [E,A] |
12 |
| [[[[F,H],C],B],[D,G]] |
9
|
The next step, somewhat
reversing the previous process, is to use the expressions in Symbol to construct
a binary tree code.
| Symbol |
Code |
| [E,A] |
0 |
| [[[[F,H],C],B],[D,G]] |
1
|
|
| Symbol |
Code |
| E |
00 |
| A |
01 |
| [[[F,H],C],B] |
10 |
| [D,G] |
11
|
|
| Symbol |
Code |
| E |
00 |
| A |
01 |
| [[F,H],C] |
100 |
| B |
101 |
| D |
110 |
| G |
111
|
|
| Symbol |
Code |
| E |
00 |
| A |
01 |
| [F,H] |
1000 |
| C |
1001 |
| B |
101 |
| D |
110 |
| G |
111
|
|
The binary code being:
| Symbol |
Code |
| E |
00 |
| A |
01 |
| F |
10000 |
| H |
10001 |
| C |
1001 |
| B |
101 |
| D |
110 |
| G |
111 |
|
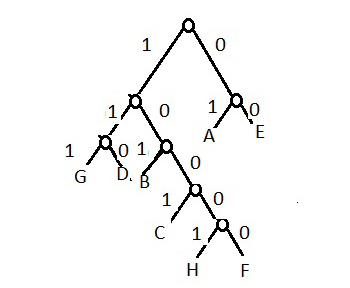 |
Comments:
- The code is balanced in terms of 1s and 0 s .
- Note that: pF ≤ pH
= pC ≤ pB
= pD ≤ pG ≤ pA ≤ pE
and
l F
≥ l H
≥ l C
≥ lB
≥ l D ≥ l G ≥ l A ≥ l E (length)
- There are two codes of longest length, in this case 5. This is not a coincidence thought there may be more than two of longest length.
- Since we are only dealing with 8 symbols, we could encode them
with binary strings of fixed length 3. However, E and A occur with
total frequency 12 but C, F, and H occur with total frequency 3.
B, D, G are encoded with binary strings of length 3 in either case. The
Huffman code is optimal in the sense that the expected length of
messages are shortest. In particular: E(transmission length) = 2*(7/21)+2*(5/21)+5*(1/21)+5*(1/21)+4*(1/21)+3*(2/21)+3*(2/21)+3*(2/21)=2.67
Exercise: Apply the Huffman
algorithm to the following symbol table. Note the lengths of the code
words and the exponents of the various probabilities .
| Symbol |
Probability |
| A |
1 /23 |
| B |
1 / 24 |
| C |
1 / 24 |
| D |
1 / 23 |
| E |
1 / 21 |
| F |
1 / 24 |
| G |
1 / 24 |




