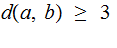How far is it from Chestnut and 11th to Locust and 9th?
"As the crow flies?"
"As the man walks?"
The "locations" we are looking at are the street intersections.
The distance
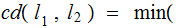 number of city blocks one has
to walk from
number of city blocks one has
to walk from
 to
to
 Chestnut
and11th , Locust and
9th
Chestnut
and11th , Locust and
9th 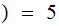
Properties:
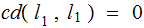
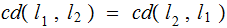
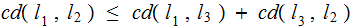
Definition: Given an alphabet of
symbols
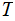 ,
and two strings
,
and two strings
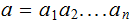 and
and
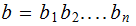 ,
of equal length, where
,
of equal length, where
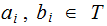 ,
,
we define the Hamming
Distance 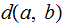 to
be the number of positions in which they differ.
to
be the number of positions in which they differ.
More formally.
If
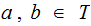 ,
, 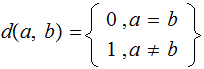

If
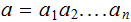 and
and
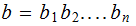 ,
of equal length, where
,
of equal length, where
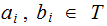 ,
,
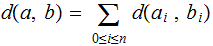
Metric Properties:
For all
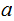 ,
,
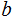 ,
and
,
and
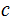 :
:
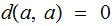
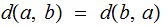
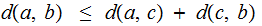
Assume
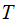 is
the alphabet of code symbols to be transmitted and the valid code words
,
is
the alphabet of code symbols to be transmitted and the valid code words
,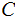 , are all of the same length.
, are all of the same length.
For
example: in ASCII
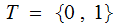 and
and
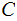 consists of 8 bit strings where the 8th bit is an odd or even parity bit.
consists of 8 bit strings where the 8th bit is an odd or even parity bit.
Making the artificial assumption that a transmitted code word can have at most 1 error:
Assuming the Hamming Distance between valid code words is at least 2:
Transmission errors can be detected by checking the string received against the valid codes.
If the string agrees with a valid code then that was the string that was transmitted.
If it
differs by 1 from a valid code then there was a transmission
error.
Assuming the Hamming Distance between valid code words is at least 3:
Transmission errors can be corrected by checking the string received against the valid codes.
If the string agrees with a valid code then that was the code word that was transmitted.
If it
differs by 1 from a valid code then that was the code word that was
transmitted since it cannot differ by 1 from another valid code.
The Calculation:
Suppose
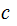 differs
by 1 from two valid code words
differs
by 1 from two valid code words
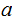 and
and
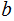 :
:
Then
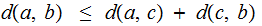
But
if
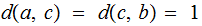 ,
,
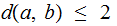
But
the assumption is that