A brief review of basic time complexity and asymptotic bounds

The exact running time of an algorithm is usually a complex expression. In order to simplify things, normally the run time is estimated using asymptotic notation.

The most common type of asymptotic notation used is called big-O notation.

Asymptotic notation uses only the highest order term of the expression for the algorithm’s running time. No coefficient is used, and all lower order terms are ignored.

EXAMPLE: f (n) = 42n³ + n² – 8n + 5712. We say that f (n) = O(n³) and that n³ is the asymptotic upper bound for f (n).

Many times, we derive bounds of the form n^c for c greater than 0. These are called polynomial bounds.

Bounds of the form 2⁽⁾ are called exponential bounds when k is a real number > 0.

Algorithm analysis consists of analyzing each part of the algorithm individually to determine how many steps it has, then taking the sum of steps in all the parts of the algorithm.

EXAMPLE: If the parts of an algorithm have n+1 steps, 5n steps, n³ steps, and 7 steps, then the overall complexity of the algorithm is O(n³).

Time Complexity and Complexity Theory

Let t: N→R⁺ be a function. Define the time complexity class, TIME(t(n)), to be the collection of all languages that are decidable by an O(t(n)) time Turing machine.

In complexity theory, we classify computational problems according to their time complexity. But, the choice of model affects the time complexity of languages. Therefore, the same language may have different time requirements on different models.

EXAMPLE: Multitape Turing machine vs. single-tape Turing machine.

Let t(n) be a function, where t(n) > n. Then every t(n) time multitape Turing machine has an equivalent O(t²(n)) time single-tape Turing machine.

The proof of this is straightforward. All of the tapes of the multitape Turing machine (which we will call M) must be stored on the single-tape Turing machine (let’s call it S). Any time the length of data on one of the tapes of M increases, all of the corresponding data of the tape of S must be shifted.

This means that for each step of (t(n)) steps on M, O(t(n)) steps occur on S. Therefore, the running time of S is O(t²(n)).

Therefore, the time complexity of a single-tape Turing machine and a multitape Turing machine have a square difference.

EXAMPLE: Nondeterministic single-tape TM vs. deterministic single-tape TM.

Let t(n) be a function, where t(n) > n. Then every t(n) time nondeterministic single-tape Turing machine has an equivalent 2^O(t(n)) time deterministic single-tape Turing machine.

Skipping the proof for this, a simple yet understandable explanation for this is that the construction of a deterministic TM (D) to simulate the nondeterministic TM (N) results from searching N’s computation tree.

Even if a multitape TM is used, D still has the same time complexity. Because a conversion from a multitape TM to a single-tape TM at most squares the running time,

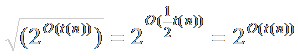
Polynomial differences in running time are considered to be small, whereas exponential differences are considered to be large. This is because of their respective growth rates.

It is for this reason that, for larger problems and larger inputs, the difference between using a single-tape TM and a multitape TM is negligible.

Furthermore, all reasonable deterministic computational models are polynomially equivalent. This means that any one of them can simulate another with only a polynomial increase in running time.