





1951 -The UNIVAC -1 was 25 feet by 50 feet
in length, contained 5,600 tubes, 18,000 crystal diodes, and 300 relays. It
had an internal storage capacity 1,000 words or 12,000 characters.. Its
reported processing speed was 0.525 milliseconds for
arithmetic functions, 2.15 milliseconds for multiplication and 3.9
Milliseconds for division. The UNIVAC was also the first computer to come
equipped with a magnetic tape unit and was the first computer to use buffer
memory.
1954 -The IBM 704 mainframe (image courtesy of
LLNL) - 4,000 instructions per second 18 kilobytes main
memory
1982 - The Osborne Executive - 4 MHz CPU
124 kilobytes main memory
2012 -The iPhone 5: Processor: Dual core,
1300 MHz, System memory: 1016 MB RAM Built-in storage:16 GB
The far future: As seen in
Brazil
a "science fiction" movie (1985)
.
Moore's Law asserts that the speed of computation of a single processor will double approximately every two years. Informally, we can do twice as much work in the same time, or the same amount of work in half the time.
Moore's Law is good news! We can do a computation for "small" datasets. We need to do the same computation, for a larger dataset, but lack computers of sufficient power. Moore's Law tell us when such computations will be possible.
Moore's Law is bad news! Because there is not sufficient compute-power available,we know others are not able to do in a useful way, a certain computation that we do not want them to do. Moore's Law warns us when such computations will be possible.
Terminology:
A Moore Cycle will to refer to:
The engineering time cycle required to develop a processor capable of doing
twice the number of basic operations per "clock tic" that can be done with
today's processors. Read
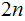 years for
years for
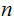 Moore cycles. Informally, it suffices to have table-lookup or a comparison in
mind when thinking about the term "basic operation."
Moore cycles. Informally, it suffices to have table-lookup or a comparison in
mind when thinking about the term "basic operation."
or
The additional number of processors (measured in powers of
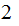 )
required to do twice the number of "basic operations" per "clock tic" that can
be done with a cluster of a given size. Using this "Moore cycles", in this
context requires a good deal of care. See
Amdahl's
Law which considers speed up possible by parallelizable components vs.
serial components of algorithms.
)
required to do twice the number of "basic operations" per "clock tic" that can
be done with a cluster of a given size. Using this "Moore cycles", in this
context requires a good deal of care. See
Amdahl's
Law which considers speed up possible by parallelizable components vs.
serial components of algorithms.
The term Computational Intractability refers to the phenomenon that many problems seem inherently impossible to solve on current computational models.
1. Addition
Consider the following template for addition
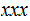
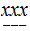
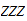
Setting aside carries, it requires
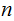 addition table lookups to add to
addition table lookups to add to
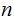 digit numbers. That is, if it is practical to add two
digit numbers. That is, if it is practical to add two
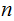 digit numbers today, in two years or in 1 Moore Cycle it
will be practical to add two
digit numbers today, in two years or in 1 Moore Cycle it
will be practical to add two
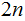 digit
numbers.
digit
numbers.
2. Multiplication
Consider the following template for multiplication.
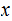 |
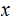 |
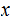 |
||
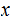 |
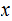 |
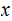 |
||
| - | - | - | - | - |
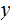 |
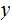 |
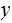 |
||
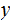 |
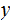 |
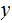 |
||
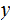 |
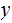 |
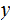 |
||
| - | - | - | - | - |
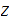 |
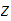 |
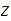 |
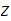 |
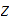 |
Setting aside all sorts of arithmetic, it requires
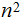 multiplication table lookups to multiply to
multiplication table lookups to multiply to
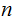 digit numbers. That is, if it is practical to multiply two
digit numbers. That is, if it is practical to multiply two
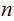 digit numbers today, in 2MooreCycles it will be practical to
multiply two
digit numbers today, in 2MooreCycles it will be practical to
multiply two
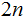 digit
numbers.
digit
numbers.
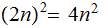 so
we will have to do 4 times as many operations.
so
we will have to do 4 times as many operations.
Let
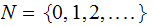 be
the natural numbers,
be
the natural numbers,
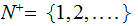 the
positive integers, and
the
positive integers, and
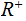 be the positive real numbers.
be the positive real numbers.
Given
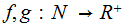 we
write
we
write
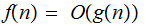 if
there exists
if
there exists
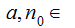
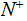 such
that.for
such
that.for
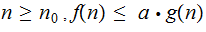
Example:
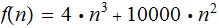 then
then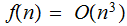
Choose
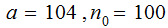
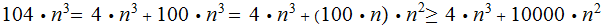 for
for
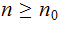
| Name | Notation |
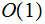 |
constant |
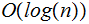 |
logarithmic |
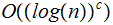 |
polylogarithmic |
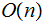 |
linear |
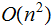 |
quadratic |
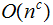 |
polynomial |
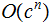 |
exponential |
Note: In specifying a Big O Notation Category for a function we choose the best possible.,
Exercise (Due April 18):
What Category is
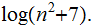
Ans: For
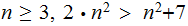
So
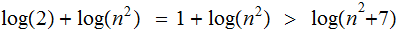
also
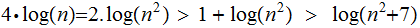
Choosing
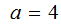 and
and
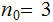 ,
we have
,
we have
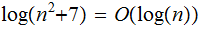
Suppose your computer can perform 10,000,000 Integer long divisions per second ( don't worry about integer size). Suppose you know
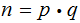 ,
a product of primes is a 400 digit integer. Worst case, brute
force, approximately how long would it take to factor
,
a product of primes is a 400 digit integer. Worst case, brute
force, approximately how long would it take to factor
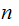 ,
remember, you only have check up
to
,
remember, you only have check up
to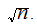
Ans: Very roughly
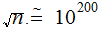 so it will take
so it will take
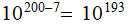 seconds.
There approximately are
seconds.
There approximately are
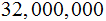 seconds in a year. So we would need more than
seconds in a year. So we would need more than
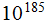 years.
years.
The Tower of Hanoi:

The object is to move the disks from one peg to any other, one disk at a time and never putting a smaller disk on top of a bigger disk.( The Applet):
Solution:
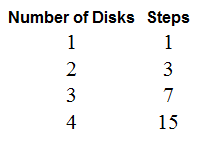
Computation: It requires
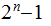 moves
to solve the
moves
to solve the
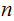 disk Tower of Hanoi problem:
disk Tower of Hanoi problem:
Notationally, if
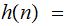 number
of moves to solve the
number
of moves to solve the
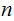 disk
problem,
disk
problem,
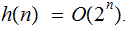
It is true for the
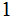 disk problem.
disk problem.
Suppose we know this to be true for the
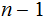 disk problem Then to solve the
disk problem Then to solve the
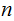 disk problem
disk problem
Move the top
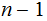 disks to a peg
in
disks to a peg
in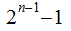 moves
moves
Move the bottom disk in
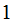 move
to the open peg..
move
to the open peg..
Move the top
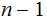 disks onto the bottom disk in
disks onto the bottom disk in
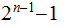 moves
moves
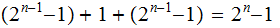
So it is practical to solve the
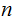 disk Tower of Hanoi problem today, in 1 Moore Cycle it will
be practical to solve the
disk Tower of Hanoi problem today, in 1 Moore Cycle it will
be practical to solve the
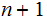 disk
problem . If I can solve the 52 disk problem today it will
require 100 Moore Cycles (200 years or lots of processors)
before I can solve the 152 disk problem.
disk
problem . If I can solve the 52 disk problem today it will
require 100 Moore Cycles (200 years or lots of processors)
before I can solve the 152 disk problem.
Breaking RSA Encryption:
We are given
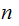 which
we know to be
which
we know to be
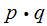 where
where
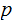
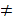
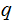 are primes. We wish to compute
are primes. We wish to compute
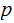
 and
and
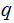 If we could, then it would be easy to compute
If we could, then it would be easy to compute
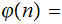
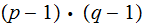
We are given
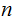 as in 1. and we just wish to
compute
as in 1. and we just wish to
compute
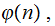 the number of members of
the number of members of
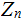 relatively
prime to
relatively
prime to
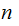 ,
, but
we don't care about
but
we don't care about
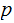
 and
and
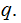 .
.
The Claim: If we can find an easy way to
compute
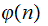 without
having to find
without
having to find
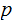
 and
and
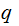 , then
finding
, then
finding
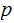
 and
and
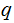 is
a simple additional calculation.
is
a simple additional calculation.
In terms of Intractability, it is just as hard to compute
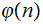 as
it is to factor
as
it is to factor
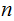 .
.
The Calculation:
Suppose we have somehow computed
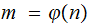 .
We then have two equations in two unknowns
.
We then have two equations in two unknowns
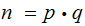
and by the the Fermat--Euler Theorem
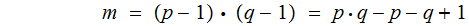
substituting
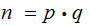 into
the second equation and solving for
into
the second equation and solving for
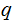
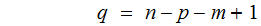
substituting this back into the first equation gives the following quadratic
equation in
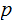
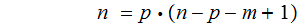
or
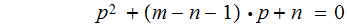
While understanding RSA and ELGlamal Encryption does require a reasonable
mathematical background. Elliptic Curve Encryption involves an understanding
of material usually reserved for advanced undergraduates, even beginning
graduate students in Mathematics. The following table provides some insight in
what Elliptic Curve Encryption offers. The counts are in bytes and each line
represents key size required to achieve a certain level of security. Finally,
for various reasons, the sizes should be considered suggestive rather that
some precise experimental comparison.
| Private Key | Public Key RSA |
Public Key Elliptic Curve |
| 10 | 10 | 20 |
| 14 | 256 | 28 |
| 16 | 384 | 32 |
| 24 | 960 | 48 |
| 32 | 1920 | 64 |
RSA implementation might be thought of as an example of the Moore's Law paradox. If we postulate that key byte size translates to compute-power required to implement the associated encryption/decryption protocols and if we think of the first and third column key sizes as somehow tracking Moore's Law, the cost of implementing RSA in terms of hardware etc. required to implement RSA key security in an efficient way, continues to increase.with every Moore Cycle.