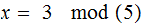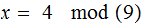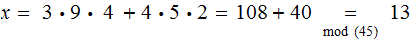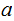 and
and
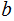 be two integers. Let
be two integers. Let
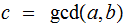 ,
the greatest common divisor of
,
the greatest common divisor of
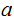 and
and
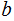 . We can find integers
. We can find integers
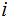 and
and
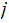 and such that
and such that
Theorem:
Let
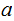 and
and
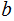 be two integers. Let
be two integers. Let
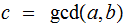 ,
the greatest common divisor of
,
the greatest common divisor of
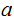 and
and
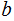 . We can find integers
. We can find integers
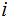 and
and
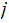 and such that
and such that

Proof:
By reordering if necessary, we can assume
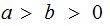 and
and
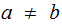 since,
since,
if
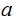 or
or
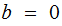 ,
the statement is trivial.
,
the statement is trivial.
if
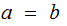 then
then
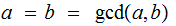 and
and
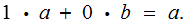
if we can prove it under this assumption then the general case follows, using
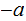 and/or
and/or
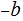 .
.
Let
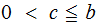 be
the smallest integer such that there are integers
be
the smallest integer such that there are integers
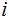 and
and
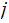 and
and
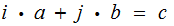 .
.
We need to show
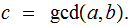
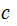 is
a common divisor of
is
a common divisor of
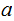 and
and
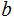 . If not, assume it does not divide
. If not, assume it does not divide
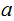 (
(
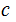 does
not divide
does
not divide
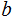 is essentially the same argument) , we have
is essentially the same argument) , we have
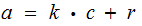 with
with
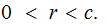
So

and
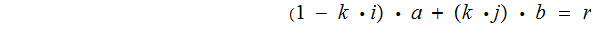
On the other hand, If
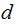 is
a common divisor of
is
a common divisor of
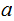 and
and
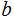 then
then
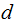 divides
divides
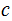 . Since
. Since
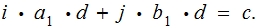
Therefore
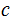 is the greatest common divisor
is the greatest common divisor
Again assume
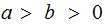 ,
if
,
if
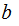 divides
divides
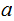 we are done since
we are done since
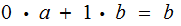 .
If not
let
.
If not
let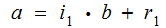 with
with
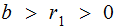 .
.
If
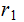 divides
divides
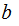 ,
it must also divide
,
it must also divide
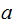 ,
so let
,
so let
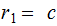 , and
, and
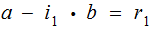
Suppose
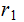 does
not divide
does
not divide
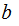 then
then
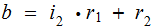 with
with
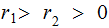 .
.
If
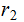 divides
divides
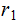 ,
as before, it also divides
,
as before, it also divides
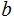 and
hence
and
hence
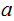 .
By back substitution
.
By back substitution
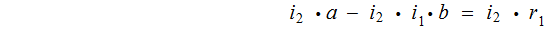
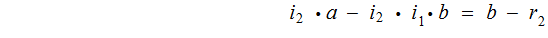
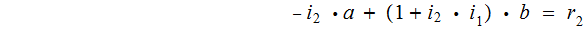
Suppose
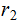 does
not divide
does
not divide
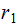 then
then
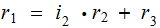 with
with
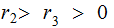 and
so on. The process must terminiate in a finite number of
steps.
and
so on. The process must terminiate in a finite number of
steps.
Corrollary:
In the setting above, again assuming
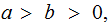 we
can select
we
can select
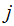 such that
such that
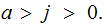
Proof: Exercise.
If
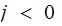 ,begin
by finding an
,begin
by finding an
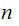 and
and
 such that
such that
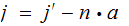
Definition:
Let
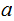 and
and
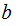 be
two integers such that
be
two integers such that
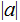
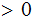 ,
,
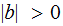 ,and
,and
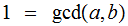 then
then
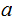 and
and
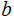 are
said to be relatively
prime
are
said to be relatively
prime
Theorem:
Let
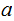 and
and
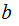 be
relatively prime Let
be
relatively prime Let
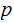 be a prime such that
be a prime such that
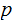 divides
divides
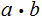 .
Then divides
.
Then divides
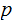 divides
divides
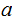 or
or
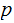 divides
divides
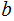
.
Proof:
Suppose
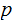 does not divide
does not divide
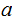 , then we can find
, then we can find
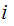 and
and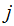 such that
such that
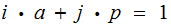
Multiplying both sides of the equation by
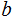 ,
we have
,
we have
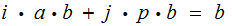
Since
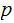 divides both terms on the left side of the equation,
divides both terms on the left side of the equation,
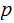 divides
divides
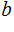
Theorem:
Every integer
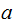 such
that
such
that
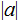
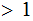 can be uniquely factored into a product of primes (perhaps times
can be uniquely factored into a product of primes (perhaps times
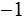 )
)
Proof:
First show by an inductive argument that every such integer is either a prime or a product of primes. Then use the previous Theorem to show that the product is unique.
Godel Numbers - An Example:
Working with {A,B,C....,Z} coded as
 {1,2,3....,25,26}
and the sequence of prime numbers
{1,2,3....,25,26}
and the sequence of prime numbers
 {2,3,5,7,11,.......}
where the
{2,3,5,7,11,.......}
where the
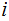 th prime is denoted by
th prime is denoted by
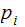 .
.
encode a sequence of letters ,again as numbers,
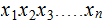 as a single integer
as a single integer
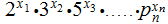 . Because of unique factorization we can recover the original sequence.
. Because of unique factorization we can recover the original sequence.
Below, sometime our
calculations will be in
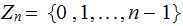 and
sometimes in the integers
and
sometimes in the integers
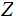 . Hopefully, use of the phases " In
. Hopefully, use of the phases " In
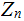 "
and " In
"
and " In
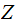 "
will clarify where the computations are taking place
"
will clarify where the computations are taking place
and the conclusions that can be draw::
Some Examples
In
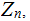 the
equation
the
equation
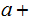
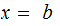 is
uniquely solvable for
is
uniquely solvable for
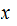 and
therefore, in
and
therefore, in
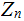 , we can also define the operation
, we can also define the operation
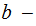
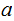 .
.
If
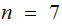 then, in
then, in
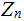 , the solution to the equation
, the solution to the equation
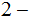
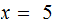 is
is
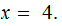 :
:
In
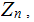 in general the equation
in general the equation
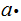
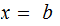 is
not solvable, however: If
is
not solvable, however: If
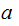 and
and
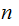 are
relatively prime, as Integers then there is a unique
are
relatively prime, as Integers then there is a unique
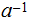 with
with
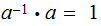 In
In
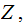 just
solve
just
solve
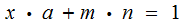 , in particular
, in particular
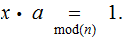 In
In
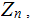 let
let
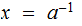
Exercise: We are assuming that,
in
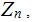 let
let
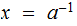 "
makes sense in terms of existance and, uniqueness, why?:
"
makes sense in terms of existance and, uniqueness, why?:
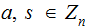 and
and
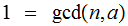 ,
as Integers, then in
,
as Integers, then in
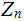 the equation
the equation
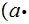
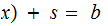 is
uniquely solvable
is
uniquely solvable
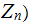 :
:
Choose
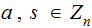 with
with
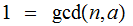 ,
, as Integers.
as Integers.
Encryption -
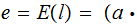
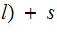
Decryption -
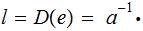
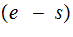
Representing the letters of the alphabet
(A,B,....,Z) as
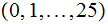 and looking at
and looking at
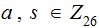 with
with
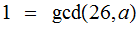 ,
, as Integers,
as Integers,
Advantages: It is easy to compute and slightly better than
the Caesar Cyper in that there are
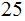 choices for
choices for
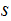 and
and
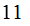 choices
for
choices
for
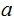 (not
(not
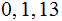 )
or
(
)
or
(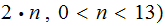 . That
is
. That
is
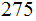 possible codes.
possible codes.
Disadvantages: It is really just a Substitution
Cypher!
Plan B: Encode the entire
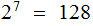 character ASCII table, and look at
character ASCII table, and look at
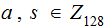 with
with
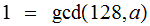 ,
, as Integers.you would want to do this anyway. Still easy to compute and now
there are approximately
as Integers.you would want to do this anyway. Still easy to compute and now
there are approximately
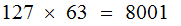 possible
codes. A bit harder but still subject to frequency analysis attacks.
possible
codes. A bit harder but still subject to frequency analysis attacks.
Plan C: Use Affine Encryption to encode data in 4 byte
blocks say, using
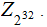 You
could encode text 4 characters at a time.
You
could encode text 4 characters at a time.
Definition: Let
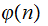 be the number of members of
be the number of members of
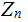 relatively
prime to
relatively
prime to
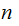 ,
as integers.
,
as integers.
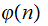 is
called the Euler Totient Function.
is
called the Euler Totient Function.
If
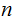 is
a prime then
is
a prime then
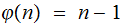
If
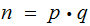 where
where
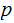
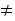
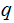 are primes then
are primes then
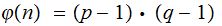 .
.
Theorem: Let
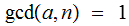 , then
, then
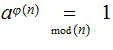
Proof: (Unless otherwise noted all calculations will be in In
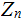 )
)
We can assume
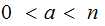 (
(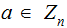 ) since if
) since if
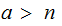 ,
and
,
and
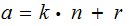 then
then
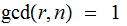 and
and
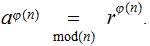
Let
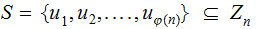 be
the subset of members relatively prime to
be
the subset of members relatively prime to
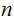 .
.
Since the
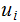 have
multiplicative inverses, one verifies that
have
multiplicative inverses, one verifies that
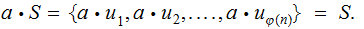
So

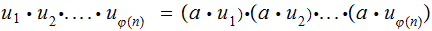
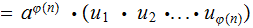
Theorem: Suppose
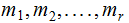 are
pairwise relatively prime positive integers,
are
pairwise relatively prime positive integers,
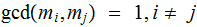 and
and
 Suppose
Suppose
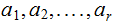 are
integers. Then the system of simultaneous equations
are
integers. Then the system of simultaneous equations
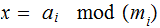
has a unique solution
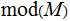 ,
where
,
where
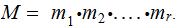
Proof: Let
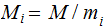 and
and
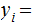
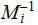
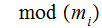 , this is well defined
, this is well defined
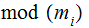 since
since
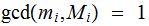
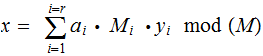
Exercise 1: Show
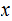 is a solution and is unique
is a solution and is unique
Exercise 2:
Let
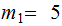 ,
,
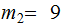 ,
,
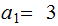 ,
,
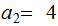 solve the simultaneous equations:
solve the simultaneous equations: