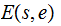 as
as
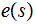 and
and
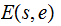 as
as
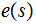 and
and
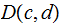 as
as
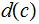 which is consistant with 1.
which is consistant with 1.
Setting: A bank wants to communicate with its customers
over the internet.
It does not want to set up different keys for each customer, a lot of work.
It does not want to risk a customers secret key being stolen or otherwise compromized.
It will be notationally convenient below to abbreviate
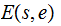 as
as
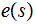 and
and
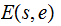 as
as
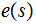 and
and
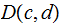 as
as
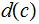 which is consistant with 1.
which is consistant with 1.
Methodology: The bank tells the world about
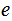 and if a customer wants to communicate a message
and if a customer wants to communicate a message
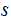 ,
,
the customer first computes
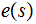 and
then transmits
and
then transmits
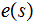 .
The bank then "receives" the message by computing
.
The bank then "receives" the message by computing
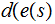 ).
).
Issues:
Knowing
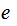 ,
it should be hard to determine
,
it should be hard to determine
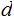 .
.
The message should still contain some private information, maybe an account number, so that a customer's account is not compromised.
Digital Signatures:
PKE can be used for two way secret communication, between bank
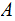 and
bank
and
bank
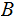 ,
as follows:
,
as follows:
Assume bank
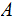 has a PKE
(
has a PKE
(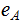 ,
,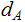 ) and bank
) and bank
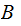 has a PKE
(
has a PKE
(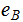 ,
,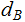 ).
).
Assume the Messages are the same for both PKEs , moreover assume
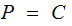 for
both.
for
both.
Finally assume,
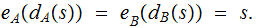
Note that this would be true for 2 RSA schemes (see below).
Methodology: bank
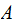 wishes
to send a secret message
wishes
to send a secret message
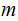 ,
using it computes
,
using it computes
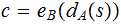 and transmits it. To read the message bank
and transmits it. To read the message bank
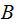 computes
computes
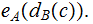
Again, bank
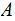 knows
knows
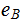 but
not
but
not
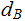 and
bank
and
bank
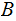 knows
knows
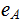 but
not
but
not
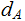 .
.
Methodology: Our calculations are in
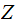 unless
noted as
unless
noted as
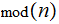 .
.
Choose
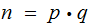 where
where
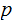
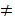
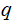 are primes and
are primes and
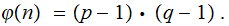
Choose
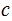 such that
such that
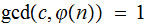 ,
and let
,
and let
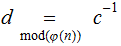 .
.
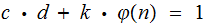 for
some
for
some
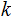 .
.
The key observation is that if
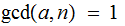 for
for
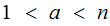 then by the Fermat--Euler Theorem:
then by the Fermat--Euler Theorem:
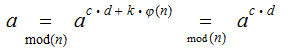
To allow anybody to securely transmit messages to
you :
:
Tell the world
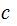 and
and
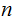 . Assume somebody wants to send the message
. Assume somebody wants to send the message
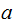 to
you privately, tell them to compute
to
you privately, tell them to compute
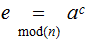 and transmit
and transmit
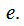
To decode the message received:
Compute
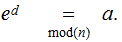
To break the code:
Since people know
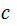 and
and
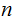 , they need to calculate
, they need to calculate
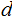 , and to do that they need to calculate
, and to do that they need to calculate
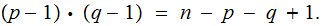
In particular factor
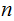 , which can be difficult.
, which can be difficult.
Some additional Notes. from a course I taught a few years back.
An original example from Rivest, Shamir, Adleman(1978):
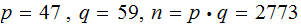
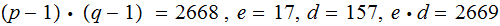
The Alphabet Encoding:
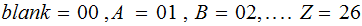
The Message:
ITS
ALL GREEK TO ME
The Message encoded in blocks of 2(with padding the last
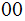 ):
):
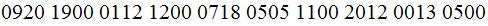
- - - - - -- - - - - -
Note: Encoding in blocks of 2 and then enciphering the block is a bit idiosyncratic. I chose to reproduce the original example.
What makes this work is that the biggest, thus encoded message
(ZZ) ,considered as a number
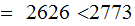
Of course, the price paid is that the deciphered message may have an extra blank at the end.
- - - - - - - - - - - - - - - - - -
IT :Enciphered
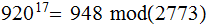
The Message Enciphered :
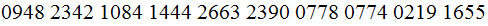
IT :Deciphered
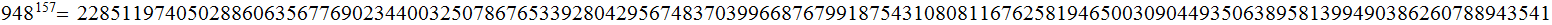
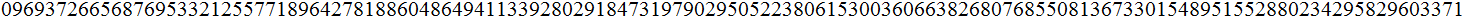
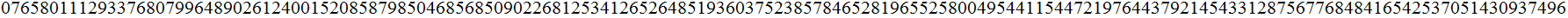
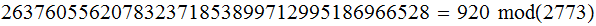
Exercise(Due April 11 )
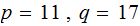
The Alphabet Encoding:
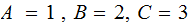
The Message:
CAB
Find an appropriate
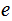 and
and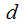 then
Encode
then
Encode
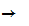 Encipher
Encipher 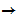 Decipher
the message.
Decipher
the message.
Definitions:
Given a prime,
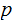 , we are looking at
, we are looking at
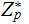 ,
the multiplicative group of non-zero elements in
,
the multiplicative group of non-zero elements in
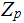 .
.
We say
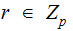 is
primitive root if
is
primitive root if
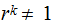 for
for
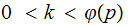 .
.
An
an example is
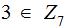 but
not
but
not
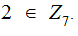
Given
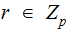 a primitive root , for any
a primitive root , for any
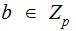 define
the discrete logarithm of
define
the discrete logarithm of
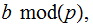 written
written
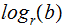 ,
to be the least positive integer
,
to be the least positive integer
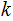 such that
such that
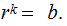
Note
Methodology:
Given
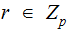 a primitive root, choose a private key
a primitive root, choose a private key
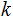 .
.
To allow
anybody to securely transmit messages to
you :
:
Tell the world
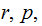 and,
and,
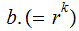 . Assume somebody wants to send the message
. Assume somebody wants to send the message
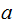 to
you privately, tell them to select a private key
to
you privately, tell them to select a private key
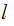 compute
compute
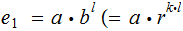
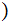 and
and
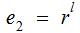 ,
and transmit both values.
,
and transmit both values.
To decode the message received:
Compute
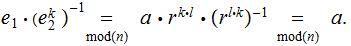
To break
the code:
Plan A: You
know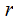 and,
and,
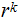 just compute
just compute
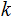 .
.
Plan B: You
know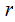 and,
and,
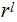 just compute
just compute
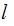 and
since you know
and
since you know
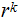 compute
compute
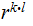 then
compute
then
compute
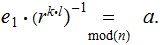
In both cases you need to be able to compute the discrete logarithm of a number. Again this is hard computationally.

This image is from Cryptography: Theory And Practice By Douglas Robert Stinson,
an excellent book for those who wish to pursue this subject further.