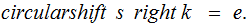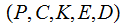 where:
where:
Definition: A Cryptosystem has
five elements
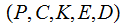 where:
where:
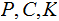 are finite sets:
are finite sets:
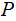 the plain text , the members of are called symbols.
We will most often use the notation
the plain text , the members of are called symbols.
We will most often use the notation
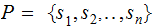 reserving
reserving
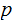 for probabilities.
for probabilities.
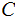 the cipher text. We will most often use the notation
the cipher text. We will most often use the notation
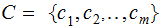
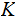 the set of keys . It is sometimes necessary to distinguish
between keys used for encryption and decrypting but when we want to refer to
keys in general we will use the
notation
the set of keys . It is sometimes necessary to distinguish
between keys used for encryption and decrypting but when we want to refer to
keys in general we will use the
notation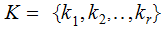
A message is a string of plain text
symbols.
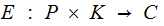 is
called the Encryption
Function.
is
called the Encryption
Function.
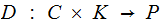 is
called the Decryption
Function.
is
called the Decryption
Function.
For each
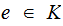 ,
there exists a key
,
there exists a key
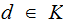 such that for any
such that for any
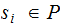
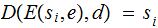
Definition: A cryptosystem is called
symmetric or private key if
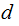 can be computed from
can be computed from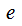 by
a simple computation, for example
by
a simple computation, for example
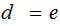 .
.
A private key cryptosystem would be used to exchange messages under the assumption that those exchanging messages could encode and decode all communications using the private key
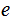 and hence
and hence
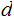 .
.
Definition: A cryptosystem is called
asymmetric or public key if
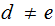 ,
and computing
,
and computing
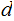 from
from
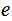 is computationally intractable, or at least very difficult.
is computationally intractable, or at least very difficult.
A public
key cryptosystem would be used for one way communication.
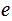 would be made public and would be used to encode messages and then communicate
them to the holder of
would be made public and would be used to encode messages and then communicate
them to the holder of
A typical use of a public key cryptosystem might be a Bank receiving information over the internet.
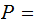 {A,B,C....,Z}
{A,B,C....,Z}
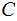
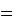 {A,B,C....,Z}
{A,B,C....,Z}
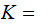 {1,2,3....,25}
{1,2,3....,25}
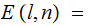 shift
right
shift
right
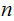 letters ,
letters ,
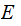 encodes
symbol by
symbol
encodes
symbol by
symbol
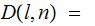 shift
left
shift
left
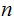 symbols.
symbols.
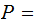 {A,B,C....,Z}
considered as members of
{A,B,C....,Z}
considered as members of
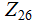 (A is 0
and Z
is 25).
(A is 0
and Z
is 25).
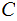
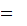 {A,B,C....,Z} considered
as members of
{A,B,C....,Z} considered
as members of
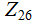
.
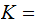 The
set of
The
set of
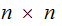 invertible
matrices in
invertible
matrices in
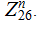
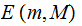 is defined as
follows:
is defined as
follows: Given
a message
Given
a message
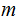 and
and
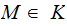 ,
by padding if necessary, write
,
by padding if necessary, write
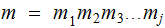
a concatenation of strings of length
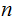 .
Let
.
Let
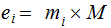 and
send
and
send
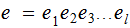 , again a concatenation of strings of length
, again a concatenation of strings of length
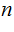
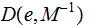 "Deconcatenate"
"Deconcatenate"

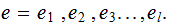 back into strings of length
back into strings of length
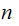 then
then

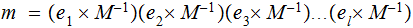
Setting:
We are given a Cryptosystem
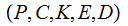 and
probability distributions
and
probability distributions
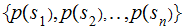 and
and
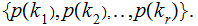
Moreover, we assume that the distributions of
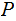 and
and
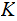 are
independent,
are
independent,
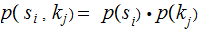 .
.
Hence we can compute
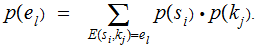
Assumptions:
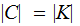 ,
, 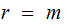 ,
the key set and cipher sets are the same size.
,
the key set and cipher sets are the same size.
The distribution
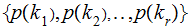 is
uniform, for all
is
uniform, for all
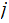 ,
, 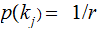
The equation
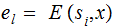 has
a unique solution for all
has
a unique solution for all
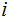 ,
,
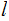 , given
, given
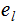 and
and
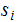 there
is a unique
there
is a unique
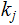 such that
such that
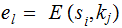 .
.
Consequences:
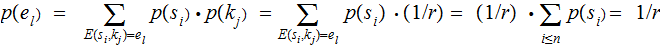 ,
,
because of Assumption
3.
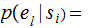
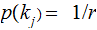 ,where
,where
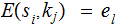 .
.
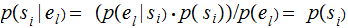
A Cryptosystem
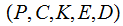 has perfect secrecy if for any
has perfect secrecy if for any
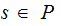 and
and
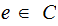
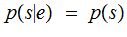
The probability that
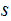 was the source symbol given that it was encoded as
was the source symbol given that it was encoded as
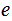 is the same as the probability that
is the same as the probability that
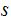 was the source symbol. Someone intercepting the code can't use it to infer the
original text.
was the source symbol. Someone intercepting the code can't use it to infer the
original text.
The Vernam
One-Time Pad:
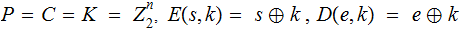 ,
where stands for vector (bit-wise) addition.
,
where stands for vector (bit-wise) addition.
Since
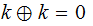 ,
,
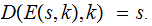
For any
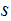 and
and
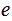 there is a unique
there is a unique
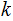 such that
such that
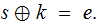 In fact
In fact
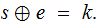
Using the One-Time Pad:
As an example, let
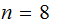 .
.
Create 2 copies of a pad, or tape, or flash drive containing a very long list
randomly generated bytes, one for each site that will be exchanging private
messages.
Suppose site A wants to send a message to site
B. Starting at the beginning of the list encode the message
byte by byte using the key bytes in sequence. When the message has been
encoded, A marks the last key byte that has been used. .
Site B receives the encoded message and, again starting with
the first key byte, decodes the message byte by byte. Also again, noting the
last byte used, which will be the same byte noted by A.
If B wants to respond to A, it begins to encode using the pad and beginning with the first unused byte.

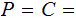 {A
,B,....Z}
{A
,B,....Z}
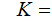 {0,1,....25}
{0,1,....25}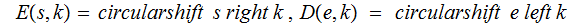
For any
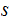 and
and
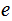 there is a unique
there is a unique
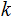 such that
such that