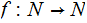 where
again
where
again
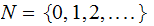 are
the natural numbers.
are
the natural numbers.
Setting:
In this section all functions will be of the form
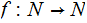 where
again
where
again
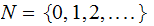 are
the natural numbers.
are
the natural numbers.
Definition The following are primitive recursive functions:
The successor function,
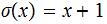 .
.
The constant functions,
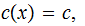 any
any
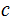
Projections,
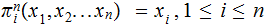 .
.
composition: Given primitive recursive functions
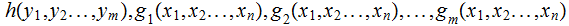 then
then
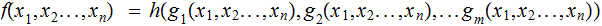
is primitive recursive:
primitive recursion: Given primitive recursive functions
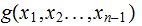 and
and
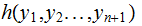
then the function
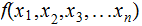 defined by the following two equations is primitive recursive:
defined by the following two equations is primitive recursive:
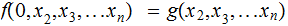
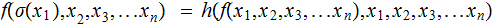
Example 1:
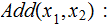
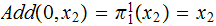
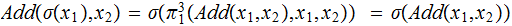
Example 2 (less formally):
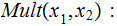
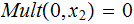
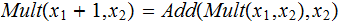
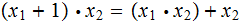
Example 3 (Exercise
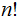 ):
):
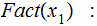
Definition: The following are partial recursive functions:
Any primative recursive function.
If
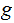 is a partial recursive function such
that
is a partial recursive function such
that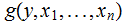 is defined for
all
is defined for
all 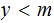 :
:
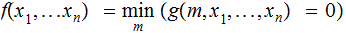
If no
such
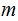 exists
then
exists
then 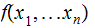 is
undefined.
is
undefined.
A partial recursive function
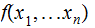 that is defined for all
that is defined for all
 is called (total) recursive.
is called (total) recursive.
There are total recursive functions that are not primitive recursive. The Ackermann Function 1 The Ackermann Function 2
Notation and Examples:
We write
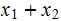 and
and
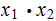 for
for
 and
and
We write
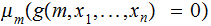 for
for
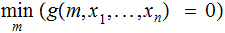
The predecessor function:
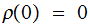
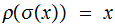
Note
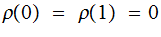
Truncated Subtraction:
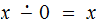
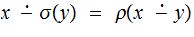
The Equals Function:
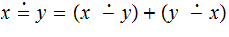
(An Aside) The C equals operator:
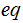 (
(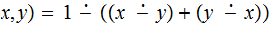
Square Root:
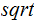 (
(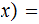
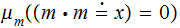
Note that
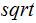 (
(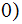 and
and
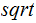 (
(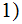 are
defined.
are
defined.
Recursive functions are identical to the set of functions
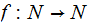 that
can mechanically computed, that is, are programmable on some deterministic
computer.
that
can mechanically computed, that is, are programmable on some deterministic
computer.

Definition :
A Turing Machine
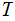 consists of:
consists of:
An alphabet
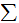 :
A finite set of symbols including
:
A finite set of symbols including
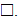
The tape: A 1 dimensional sequence of cells. Each cell is referenced by an Integer.
Each
cell can contains a single symbol from the
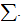 , all but a finite number of cells contain the blank symbol
, all but a finite number of cells contain the blank symbol
 .
.
At different stages of a Turing Machine computation, the tape will contain a different configuration of symbols.
A finite set of head states
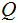 .
.
An Initial state:
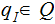
A halting state - Accept:
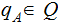 .
.
A halting state - Reject:
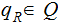 .
.
The read/write Head: In a given state
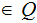 and
"positioned over" a given cell,
and
"positioned over" a given cell,
A single valued Transition Function:
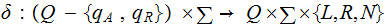 of
valid steps.
of
valid steps.
Read
if the head is in state
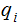 and
it is over a cell containing symbol
and
it is over a cell containing symbol
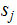 and
and
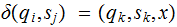 change
the symbol in the present cell to
change
the symbol in the present cell to
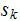 , change the head state to
, change the head state to
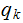 ,
,
and
move
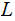 eft
or
eft
or
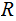 ight
one cell, or
ight
one cell, or
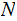 ot
at all, depending on
ot
at all, depending on
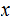 .
It is common practice to write
.
It is common practice to write
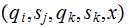 rather than
rather than 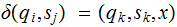 .
.
Notation:
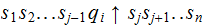 denotes
that is in state
denotes
that is in state
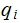 and
the tape contains the consecutive sequence of symbols
and
the tape contains the consecutive sequence of symbols
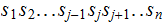 with
all blanks to the left of
with
all blanks to the left of
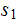 and to the right of
and to the right of
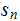 .
.
Moreover the head is over the cell containing
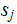 .
We call this the state of
.
We call this the state of
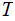 , as opposed to the head state.
, as opposed to the head state.
Given
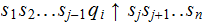 and valid step
and valid step
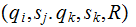 we
write
we
write
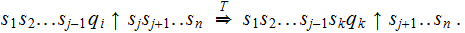 More generally
More generally
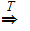 will
be used to denote a sequence of valid steps refered to as a
derivation.
will
be used to denote a sequence of valid steps refered to as a
derivation.
Alternate Definitions: There are many computationally equivalent definitions of Turing Machine..
One A: simple, in fact more commonly used, variation is as
above except in the Transition Function, rather than Head
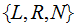 ,
only
,
only
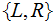 are
available.
are
available.
To create a computationally equivalent
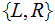 for a given
for a given
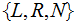 Turing Machine
Turing Machine
For
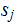 each add a new state
each add a new state
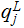 and
rules .
and
rules .
For every step of the form
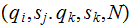 replace
it with a step,
replace
it with a step,
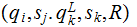 and
for each
and
for each
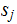 a
rule
a
rule
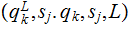
Two Another variant defines
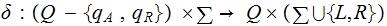 .
Here, in a given step, either the cell under the Head gets rewritten or the
Head moves not both.
.
Here, in a given step, either the cell under the Head gets rewritten or the
Head moves not both.
Exercise (Due ): Show that Two is computationally equivalent
to the original definition or to One , hence all three are
equivalent.
Three:....An n-tape Turing
Machine
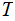 consists of:
consists of:
n tapes: each as in a single tape machine.
An alphabet
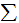 :
A finite set of symbols including
:
A finite set of symbols including
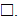 Possibly divided into per tape subsets
Possibly divided into per tape subsets
A finite set of head states
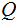 .
again as in a single tape machine
.
again as in a single tape machine
n read/write Heads: In a common state but independently positioned over each tape.
A single valued Transition Function:
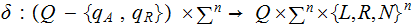 of
valid steps.
of
valid steps.
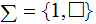
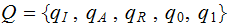
The Transition Function:
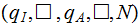 , there are no negative numbers so "
, there are no negative numbers so "
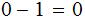 " .
" .
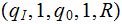
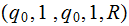
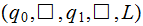
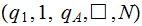
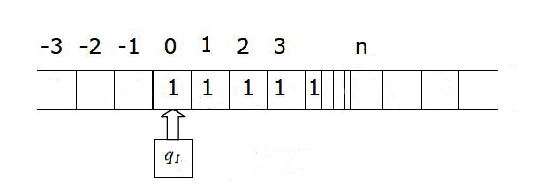
Exercise (Due May 2 ): Build a Turing Machine that
interchanges the position of two strings of
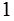 s and
s and
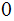 s that a separated by a single blank and with the tape blank elsewhere.
s that a separated by a single blank and with the tape blank elsewhere.
That is, starting with a tape that contains
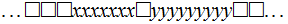 with the Head positioned over the cell containing the initial
with the Head positioned over the cell containing the initial
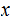 , halts when the tape contains
, halts when the tape contains
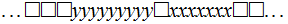 with
the Head positioned over the cell containing the initial
with
the Head positioned over the cell containing the initial
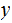 .
.
Hints:
One way to approach this problem is in terms of the Exercise just below, Build the two TMs and combine them.

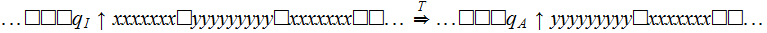
A little care has to be taken because one of the two strings may be empty (or
both, the tape could be blank)
The number of.states or symbols you use for the TM or TMs is not restricted. An symbol marking where the strings start or end might be useful.
For those of you who are building your first TM, It might be useful to build
the machines assuming the
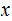 s are
s are
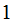 s
and the
s
and the
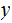 s are
s are
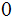 s and then modify the result for the other case.
s and then modify the result for the other case.
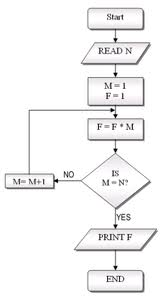
Building a TM is like writing any program, starting with an activity diagram or flow chart is usually a good idea.
Theorem(Informal):
One can show that the set of Partial Recursive Functions is identical to the set of Turing Machines computable functions.
Total Recursive Function correspond to Turing Machine computable functions that always halt.
One can enumerate the Valid Turing Machines (A program syntax checker)
An Intel Corporation Almost Universal Turing
Machine
Theorem(Informal):
One can develop a Turing Machine Description Language (TMDL). (Read "programming language").
Given a (TMDL) one can build a Universal Turing Machine
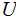 such
that:
such
that:
, If
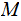 is a Turing Machine and
is a Turing Machine and
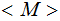 is a Turing Machine Description of
is a Turing Machine Description of
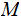 .
.
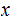 is a string that
is a string that
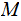 accepts then:
accepts then:

Technicalities:
There is no restriction,
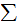 and
and
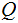 on any particular
on any particular
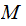 except
that they are finite sets.
except
that they are finite sets.
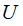 has
specific, finite
has
specific, finite
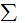 and
and
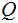 .
.
The first step in the proof of this Theorem would be developing a general alphabet encoding that could be used to encode the alphabet of any Turing Machine.
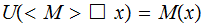 would
have to be understood in terms of that encoding.
would
have to be understood in terms of that encoding.
A Convenient 3-tape Turing Machine :
The input tape: A read-only tape containing the input, unidirectional in that its head can only move left to right;
The work tape: Where all computations are carried out, bidirectional but initially blank:
The output tape: unidirectional and Initially blank, where the result of the computation is copied from the working tape, before halting.
We say such a Turing Machine halts on
input 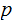 with
output
with
output 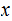 , and write
, and write
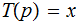 if
if
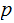 is to the left of the input head and
is to the left of the input head and
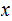 is to the left of the output head after
is to the left of the output head after
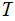 halts. .
halts. .
Exercise (Due May 2 ): (Informal, again Kolmogorov Complexity )
Given Turing Machines
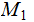 and
and
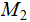 ,
and descriptions
,
and descriptions
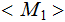 ,
,
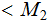 .
.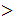 realizing functions
realizing functions
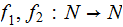 what
would a description for a Turing Machine realizing
what
would a description for a Turing Machine realizing
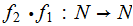 look
like. You answer should, again informally, list a series of general steps
creating the description from any
look
like. You answer should, again informally, list a series of general steps
creating the description from any
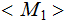 and
and
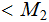 .
.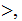 (Hint: How would you do this using Java, or C, or javascript)
(Hint: How would you do this using Java, or C, or javascript)
Yet another 3-tape variant, important for Kolmogorov Complexity, has
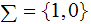 ,
,
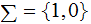 , no blank, with the work tape initally all
, no blank, with the work tape initally all
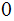 's
's
The set of
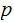 on which
on which
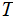 halts forms a prefix code. Such codes
halts forms a prefix code. Such codes
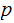 are called self-delimiting programs.
are called self-delimiting programs.
In creating a description of a Turing Machine, the halting states are replaced by some appropriate "copy to output tape" subroutine.
Note: Getting from A Convenient 3-tape UniversalTuring Machine to A Prefix Universal Turing Machine is not a huge step (see the encodings below)
"Standard" notation:For a
string 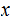 ,
,
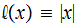
A simple prefix encoding:
For any
string 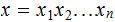 in
in
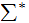 ,
define
,
define
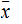 to
be
to
be
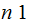 s
followed by a
s
followed by a
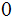 .followed
by
.followed
by
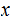 .
.
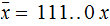 ,
,
 (
(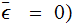
The map
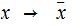 is
a prefix encoding of
is
a prefix encoding of
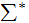 .
and
.
and
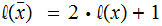
Let
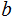 (
(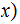 be the following binary string ordering function
be the following binary string ordering function
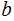 (
(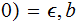 (
(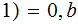 (
(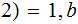 (
(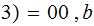 (
(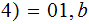 (
(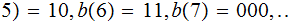
For any
string 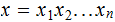 in
in
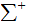 ,
,
 define
define
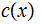 to
be the prefix encoding above, of
to
be the prefix encoding above, of
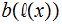
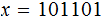
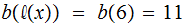
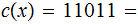
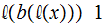 s
followed by a
s
followed by a
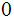 followed by
followed by
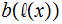 .
.
.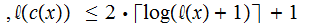 ,where
,where
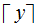 the
least
integer
the
least
integer 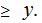
Finally
let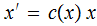 , concatinating
, concatinating
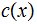 and
and
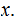
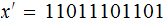
The map
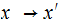 is
a prefix encoding of
is
a prefix encoding of
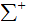 .called
the standard prefix encoding.
.called
the standard prefix encoding.
.
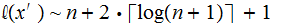 where,
again
,
where,
again
,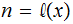 , a significant improvement. as
, a significant improvement. as
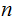 becomes large
becomes large
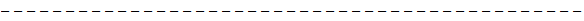
psudo code to decode
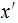
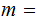 Count
Count
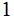 s
up to but not including first
s
up to but not including first
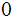 , The next
, The next
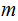 string characters, after the
string characters, after the
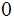 is the binary representation of the length of
is the binary representation of the length of
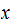 ,
call this
,
call this
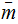 .
.
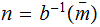
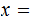 next
next
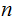 string binary digits after the first
string binary digits after the first
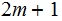
The next string begins after the first
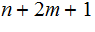
decoding
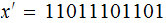
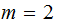 and
and
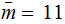
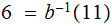
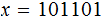
For any
string 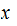 in
in
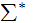
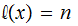 ,
let
,
let
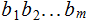 be the binary representation
of
be the binary representation
of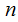 Let
Let
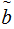
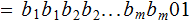 .
.
Finally let
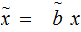
.
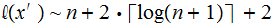
For the example above:
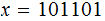
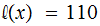
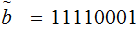
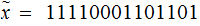
Exercise (Due May 2 ) Verify that the "standard" or simpler
short prefix encoding is indeed a prefix encoding.