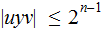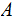 , there is a number
, there is a number
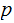 such that if
such that if
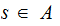 and
and
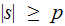
For any context-free language
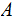 , there is a number
, there is a number
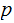 such that if
such that if
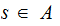 and
and
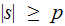
then
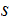 can be written as a concatination of strings
can be written as a concatination of strings
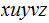 such that:
such that:
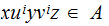 for
all
for
all
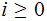
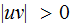 .
That is either
.
That is either
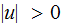 or
or
 or
both are
or
both are
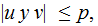
An application followed by the proof itself:
Application:
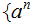
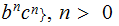 is
not a CFL.
is
not a CFL.
Proof:
If it were, applying the Theorem, neither
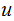 nor
nor
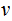 can
be a mix of
can
be a mix of
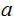 s,
s,
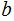 s,
and or
s,
and or
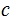 s.
Since, for example if
s.
Since, for example if
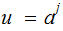
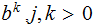 then
then
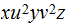 would
contain
would
contain
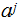
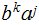
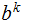 which
is not in the CFL.
which
is not in the CFL.
Thus , say
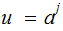 and
and
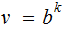 .
By 2, we know
.
By 2, we know
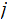 or
or
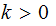 . Again
. Again
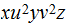 is not in the CFL.
is not in the CFL.
since the number of
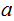 s
or
s
or
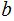 s,
or both differ from the number of
s,
or both differ from the number of
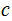 s
s
Exercise (Due April 25): Show
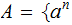
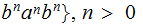 is
not a CFL.
is
not a CFL.
Answer:
Applying the Theorem, neither
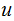 nor
nor
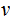 can
be a mix of
can
be a mix of
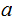 s
or,
s
or,
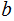 s,but
at least one must be of length
s,but
at least one must be of length
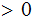 .
.
Again, going through the various cases,
if for example
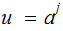 and
and
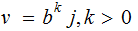 in
the first
in
the first
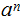 and
and
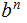 then
then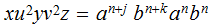 is not in the CFL
is not in the CFL
The Proof of the Theorem:
Let
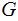 be a grammer in Chomsky Normal Form generating
be a grammer in Chomsky Normal Form generating
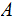 Since the two possible forms that a non-null production can take is
Since the two possible forms that a non-null production can take is
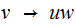 where
where
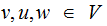 but
neither
but
neither
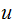 nor
nor 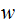 can be
can be
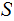
.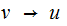 where
where
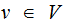 and
and
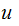 is in
is in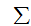
Any parse tree generated from
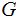 whose longest path length
is
whose longest path length
is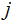 can recognize a string of length at most
can recognize a string of length at most
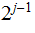
Assuming
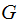 has
has
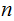 nonterminals pick a string
nonterminals pick a string
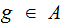 such
that
such
that
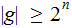 .
Any parse tree for
.
Any parse tree for
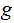 must contain a path of length greater than
must contain a path of length greater than
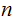 with at least one nonterminal
with at least one nonterminal
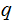 occuring more than once. The derivation would look
like.
occuring more than once. The derivation would look
like.
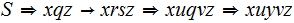 .
.
The proof follows by a simple induction on
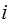 .
For example:
.
For example:
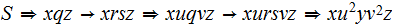
The proof of
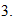 amounts
to a judicious choce of
amounts
to a judicious choce of
 ,
and of the "repeat" path .
,
and of the "repeat" path .
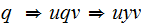
Choosing the shortest, it cannot have a sub- repeat so its length is
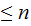 and given that Chomsky Normal Grammer strings can only add one with each
additional path step
and given that Chomsky Normal Grammer strings can only add one with each
additional path step