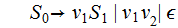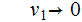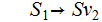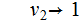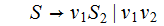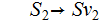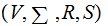 where:
where:
A Context-Free Grammar(CFG) consists of four finite sets
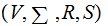 where:
where:
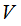 is
the set of variables.
is
the set of variables.
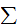 is
the set of terminals.
is
the set of terminals.
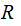 is
the set of production rules of the form
is
the set of production rules of the form
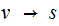 where
where
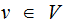 and
and
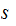 is
a string, possibly empty in
is
a string, possibly empty in
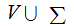
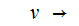 is
usually written
is
usually written
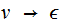 ,with
,with
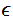 denoting the empty string.
denoting the empty string.
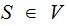 and
is the start variable.
and
is the start variable.
Terminology:
Given
 ,two
strings of variables and terminals and a production rule
,two
strings of variables and terminals and a production rule
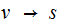 we
say that the string
we
say that the string
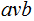 yields the string
yields the string
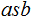 .
.
This is denoted as
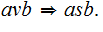
A sequence of strings of the form
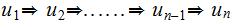 written
written
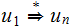 is
called a derivation and we say that
is
called a derivation and we say that
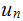 is derived from
is derived from
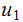
The Language of a CFG
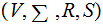 is the set of strings of terminals
is the set of strings of terminals
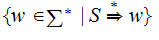
Since every step in a derivation amounts to replacing a single non-terminal by
a string, we can chose a derivation
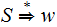
such that at each step the left-most non-terminal is replaced. This is called
a cannonical
derivation.
A Context-Free Language(CFL) is the Language of
some CFG..
A CFL containing a string
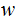 with more than one cannonical derivation is called ambigious.
with more than one cannonical derivation is called ambigious.
1.
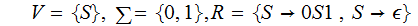
 (
( alternate
notation )
alternate
notation )
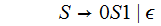
 The
Language of this CFG is
The
Language of this CFG is
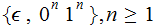 ,
for example:
,
for example:
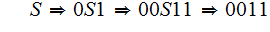
2 (Just the Rules and some notation)
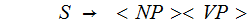
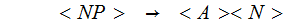
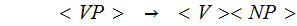
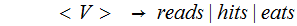

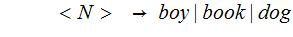
3.

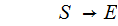
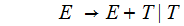
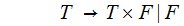
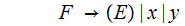
 The
Language is, algebraic expressions in
The
Language is, algebraic expressions in
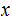 and
and
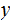 ,
for example:
,
for example:
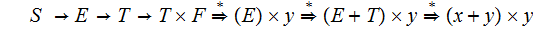
The cannonical(left) derivation:
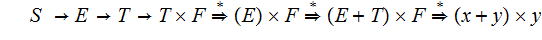
4. Ambigious
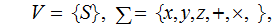
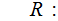
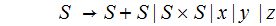
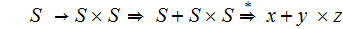
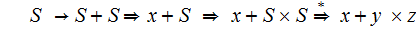
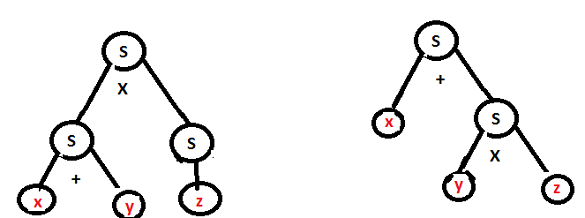
5. The Java Programming Language:
Exercise (Due April 25)
Show
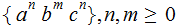 is a CFL....( eg.
is a CFL....( eg.
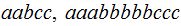 )
)
Answer:
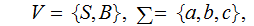
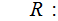
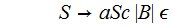
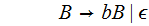
What does all of this have to do with Information Theory? - A Brief Introduction.
| Rule | Probability |
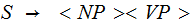 |
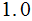 |
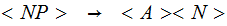 |
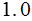 |
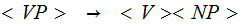 |
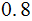 |
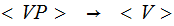 |
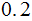 |
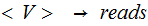 |
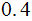 |
 |
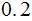 |
 |
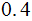 |
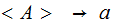 |
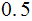 |
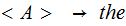 |
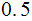 |
 |
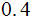 |
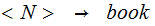 |
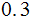 |
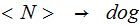 |
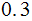 |
Read:
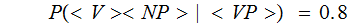 and
and 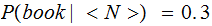
but a "standard" notation is:
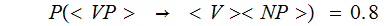 and
and 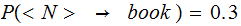
So
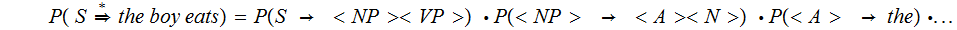
The Problem:
Kids make tasty treats.
Modifying a CFG - Removing Unit Rules:
A unit rule is a production rule of the form
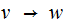 where
where
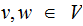
One can generate the same CFL :
By removing all unit rules,
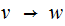 , and adding rules of the form
, and adding rules of the form
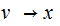 where
where
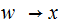 is
a rule
is
a rule
The issue is circular derivations, a sequence of rules of the form
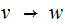 .
.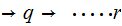 .
.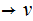
For example, if you had the rules
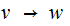 and
and
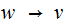 applying
the above bullet would produce a grammar with the rules
applying
the above bullet would produce a grammar with the rules
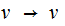 and
and
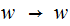 .
The solution is:
.
The solution is:
Remove all unit rules of the form
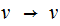
Removing all other unit rules,
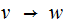 , and add rules of the form
, and add rules of the form
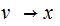 where
where
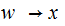 is
a rule
is
a rule
Remove all unreachable rules.
Repeat 1. and 2. and 3. until all unit rules are gone.
Example:
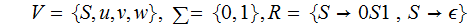
 (
(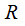 alternate
notation )
alternate
notation )
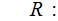
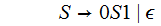
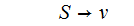
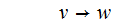
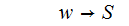
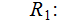
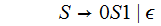
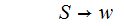
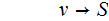
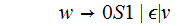
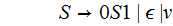
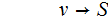
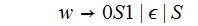 This
rule is unreachable from
This
rule is unreachable from
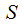 so
so
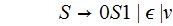
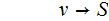
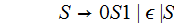
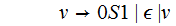 This
rule is unreachable from
This
rule is unreachable from
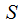 so
so
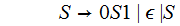 Removing
the rule
Removing
the rule
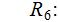
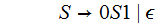 Which
is just Example 1. above.
Which
is just Example 1. above.
Definition:
A CFG is said to be in Chomsky Normal Form if every Rule is of one of three forms:
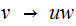 where
where
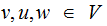 but
neither
but
neither
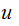 nor
nor 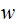 can be
can be
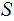
.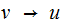 where
where
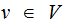 and
and
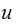 is in
is in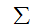
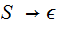
_____________________________________________________________________________
Theorem:
Context Free Languages are decidable. That is given any
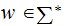 there
is an algorithm to determine whether or not
there
is an algorithm to determine whether or not
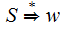
Proof:
Choose a CFG for the Language in Chomsky Normal Form.
Show that for any
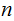 there is only a finite number of derivations
there is only a finite number of derivations
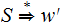 with
with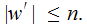
Moreover
the number of steps in each of these derivations is less than or equal to
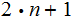 .
.
Devise an algorithm to enumerate derivations in order of increasing number
of.steps.
Check whether any derivations of step count
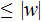 is a derivation of
is a derivation of
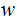 .
.
Theorem:
Any Context-Free Language can be generated by a CFG in Chomsky Normal
Form:
Proof (A sketch):
Starting with a CFG that generates the language,
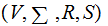 add
a new start symbol
add
a new start symbol
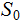 and a new Rule
and a new Rule
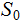
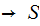 this does not change the CFL and takes care of the last part of 1. We now
refer to
this does not change the CFL and takes care of the last part of 1. We now
refer to
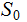 as
the start variable.
as
the start variable.
Remove any Rule of the form
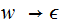 ,
,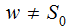 and
for any Rule of the form
and
for any Rule of the form
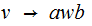 add
the rule
add
the rule
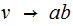 . You might have to iterate this process. You could have
. You might have to iterate this process. You could have
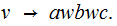
If you have a Rule of the form
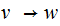 add the rule
add the rule
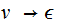 ,
again iterate if necessary.
,
again iterate if necessary.
Remove all unit rules of the form
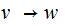 with
with
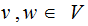 and
add rules of the form
and
add rules of the form
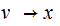 where
where
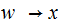 is
a rule. Again, you might have to iterate this process.
is
a rule. Again, you might have to iterate this process.
Replace rules of the form
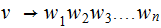 where
where
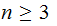 and
and
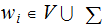 by sequences of rules
by sequences of rules
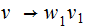 ,
,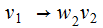 ,....,
,....,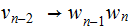 , where the
, where the
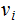 are new variables.
are new variables.
Finally any rule of the form
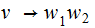 with
with
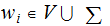 and,
say,
and,
say,
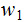
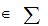 gets
replaced by two rules
gets
replaced by two rules
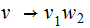 and
and
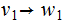 where
where
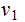 is
new variable.
is
new variable.
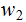
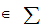 similarly.
similarly.
An Example (1. Above):
Step 1:
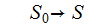
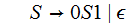
Step 2:
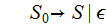
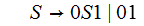
Step 3:
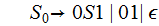
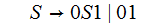
Step 4:
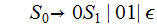
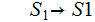
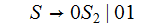
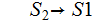
Step 5: