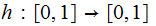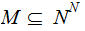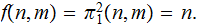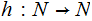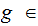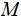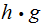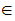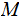Diagonal Arguments and A Fixed Point Theorem
The Liar
Paradox
A man says that he is lying; is what he says true or
false?
Eubulides of Miletus
Fourth Century B.C. Greek philosopher
The Barber Paradox
In a village lives a barber, the barber shaves everyone
living in the village who does not shave himself, but no one else.
Who shaves the
barber?
Russell's
Paradox
Bertrand Russell
British philosopher and Mathematician
The Mathematical Version, Russell's Paradox, was critical to
the understanding of the importance of formalism in Mathematics.
In his work he refered to:
Berry's Paradox
What is the least integer not describable in fewer than
thirteen words?
_______________________________________________________________________________________________________________
A Really Super Computer:
-
The Computer -
The computer we are looking at is standard except that it has unlimited
memory. Somehow it can grab as much memory as it needs to do calculations. The
bytes in memory are ordered by the Natural Numbers
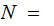 {0,1,2....} .
I am not claiming that the computer is fast, just that it is as big as it
needs to be to make any calculation.
{0,1,2....} .
I am not claiming that the computer is fast, just that it is as big as it
needs to be to make any calculation.
-
Target Programs - We are working with some
general purpose language Java, C , C++, however, we want to think of the
program as compiled and sitting inside our computer in a consecutive sequence
of bytes, therefor we can think of a program as a single (binary) number
sitting in computer memory. We use
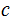 to denote such a program/number. We can think of programs have an order given
by their representation as numbers.
to denote such a program/number. We can think of programs have an order given
by their representation as numbers.
The programs we are interested are those that realize functions of the form
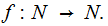 That is, if we load
That is, if we load
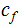 into
our computer, write
into
our computer, write
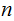 in the appropriate place in memory, and start the program, after a while the
program halts and we find
in the appropriate place in memory, and start the program, after a while the
program halts and we find
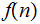 in the appropriate place in memory.
in the appropriate place in memory.
-
The Program
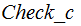 -
This program accepts as input a Natural Number and returns
-
This program accepts as input a Natural Number and returns
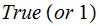 if
is one of our target programs and
if
is one of our target programs and
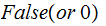 if it is not. Again everything is to be thought of as taking place in
The Computer. We will write
if it is not. Again everything is to be thought of as taking place in
The Computer. We will write
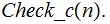
-
The Program
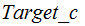 -
This program accepts as input a Natural Number
-
This program accepts as input a Natural Number
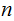 and returns the number
and returns the number
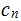 ,
the internal representation, of the
,
the internal representation, of the
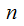 th
Target Program. We write
th
Target Program. We write
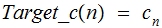
Some psudo-code for
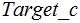 :
:
Target_c(
n ){
int
i=0, j=0;
while(True){
if(
Check_c(i)){
if(
j == n )return i;
j++;
}
i++;
}
}
-
The Program
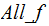 -
This program accepts as input two Natural Numbers
-
This program accepts as input two Natural Numbers
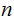 and
and
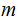 .
Computes
.
Computes
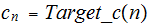 and
then computes
and
then computes
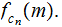
that is
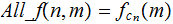
The Problem: No matter how super our super
computer is,
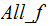 cannot
be written.
cannot
be written.
Proof: Consider the function
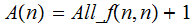 If
If
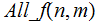 can
be programmed, so can
can
be programmed, so can
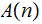 ..
Let
..
Let
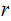 be such that
be such that
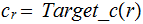 is the corresponding internal representation of
is the corresponding internal representation of
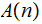 .
.
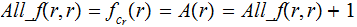
The problem is
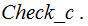
______________________________________________________________________
The Halting Problem:
Question: Can we write a Program
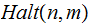 ,
such that given any syntatically correct program, again thought of as a number
,
such that given any syntatically correct program, again thought of as a number
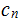 ,
and an input to that program, determines if the program will eventually
halt on input
,
and an input to that program, determines if the program will eventually
halt on input
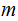 ?
?
Answer: No, similar to the argument above, except define
.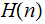 such that:
such that:
______________________________________________________________________
The Fixed Point Theorem
The Setting:
The Theorem:
Suppose we are given two sets
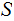 and
and
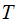 and a
map
and a
map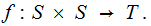
Let
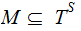 be
the set of maps
be
the set of maps
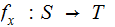 where
where 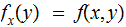 .
.
Then any function
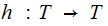 such
that
such
that
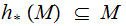
 has a fixed point.
has a fixed point.
 In
particular, for some
In
particular, for some
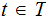 ,
,
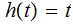
Proof:
Under these assumptions
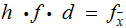 for some
for some
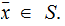 So
So
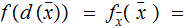
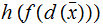 ,
,
 In
particular,
In
particular, 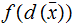 is a fixed point of
is a fixed point of
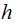 .
.
_______________________________________________________________________
Corollary 1.
Suppose we have any set
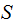 with
more than 1 member then there is no map
with
more than 1 member then there is no map
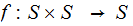 , such
that
, such
that
for any
.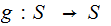 there
is an
there
is an
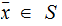 such
that
such
that 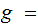
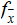
Proof:
Following the notation above, thinking
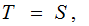 that
that

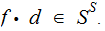 is more or less by definition, it is certainly a
map.
is more or less by definition, it is certainly a
map.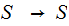
Also by definition for any
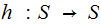 ,
,
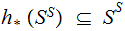 , here
, here
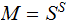
Since
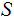 has at least 2 members, choose any map
has at least 2 members, choose any map
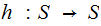 without a fixed point contradicting conclusion of the Theorem.
without a fixed point contradicting conclusion of the Theorem.
______________________________________________________________________________
Corollary 2.
The is no (total) recursive function
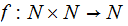 such
that for any (total) recursive
function
such
that for any (total) recursive
function 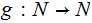 there is an
there is an
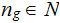 such that
such that
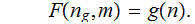
Proof:
-
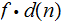 formally
formally
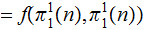 is
recursive.
is
recursive.
-
The successor function,
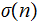 has no fixed point. and again the set of recursive functions is closed under
composition.
has no fixed point. and again the set of recursive functions is closed under
composition.
_______________________________________________________________________________
Corollary
3. There is no
continuous function from the real line onto the set of continuous real valued
functions.
Proof:
Use the fact that
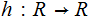
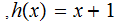 does not have a fixed point.
does not have a fixed point.
Here a cardinality argument does not work since the cardinality of the set of
continuous real valued functions is the same as that of the Reals.
________________________________________________________________________________
NOT Corollary 4.
Theorem
Primitive Recursive Functions ARE Recursively Enumerable
Proof:( See)
________________________________________________________________________________
NOT Corollary 5.
There is no continuous function from the unit interval
![$\QTR{Large}{[0,1]}$](graphics/FixedPoint__120.png) onto the set of continuous real valued functions from the unit interval to
itself.
onto the set of continuous real valued functions from the unit interval to
itself.
Proof:
Lots of easy proofs but every continuous function
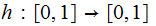 does
have a fixed point.
does
have a fixed point.
________________________________________________________________________________
(Exercise Due May 2) NOT
Corollary 6.
 and
and
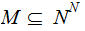 are
the constant functions These are even primitive recursively
enumerable
.
are
the constant functions These are even primitive recursively
enumerable
.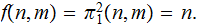
Moreover if
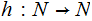 is any function and
is any function and
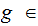
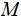 so
is
so
is
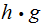 ,
,
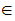
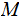 Yet the Theorem itself does not apply. Why?
Yet the Theorem itself does not apply. Why?
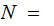 {0,1,2....} .
I am not claiming that the computer is fast, just that it is as big as it
needs to be to make any calculation.
{0,1,2....} .
I am not claiming that the computer is fast, just that it is as big as it
needs to be to make any calculation.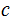 to denote such a program/number. We can think of programs have an order given
by their representation as numbers.
to denote such a program/number. We can think of programs have an order given
by their representation as numbers.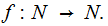 That is, if we load
That is, if we load
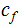 into
our computer, write
into
our computer, write
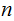 in the appropriate place in memory, and start the program, after a while the
program halts and we find
in the appropriate place in memory, and start the program, after a while the
program halts and we find
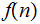 in the appropriate place in memory.
in the appropriate place in memory.
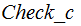 -
This program accepts as input a Natural Number and returns
-
This program accepts as input a Natural Number and returns
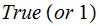 if
is one of our target programs and
if
is one of our target programs and
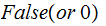 if it is not. Again everything is to be thought of as taking place in
The Computer. We will write
if it is not. Again everything is to be thought of as taking place in
The Computer. We will write
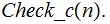
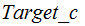 -
This program accepts as input a Natural Number
-
This program accepts as input a Natural Number
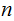 and returns the number
and returns the number
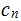 ,
the internal representation, of the
,
the internal representation, of the
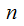 th
Target Program. We write
th
Target Program. We write
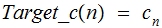
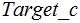 :
:
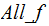 -
This program accepts as input two Natural Numbers
-
This program accepts as input two Natural Numbers
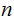 and
and
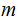 .
Computes
.
Computes
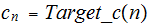 and
then computes
and
then computes
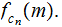
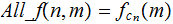
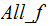
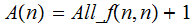
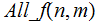
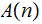
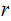
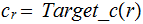
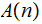
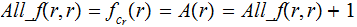
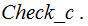
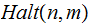
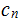
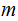
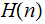
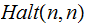
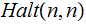
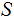
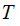
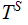
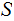
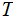
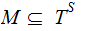
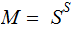

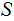
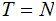
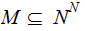
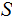
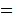
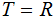
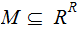
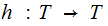
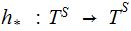
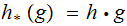
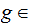
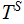
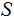
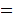
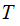
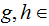
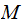
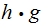
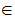
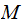
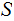
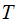
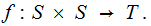
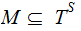
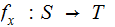
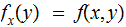
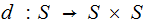
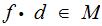

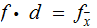
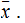
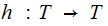
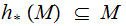


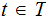
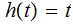
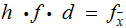
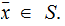
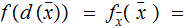
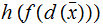

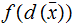
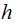
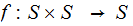
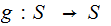
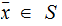
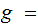
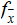
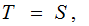

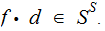
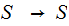
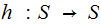
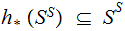
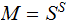
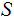
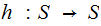
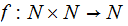
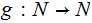
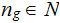
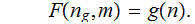
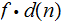
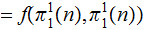
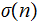
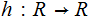
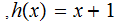
![$\QTR{Large}{[0,1]}$](graphics/FixedPoint__120.png)