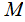 that halts on all inputs, the time complexity of
that halts on all inputs, the time complexity of
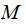 is
the function
is
the function
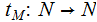
Given a Turing
Machine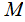 that halts on all inputs, the time complexity of
that halts on all inputs, the time complexity of
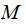 is
the function
is
the function
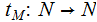
where:
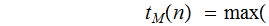 number
of steps such that
number
of steps such that
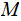 halts
on an input of length
halts
on an input of length
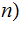
Since Turing Machine alphabets are finite, hence there is only a finite number
of strings of any
length.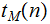 is well defined:
is well defined:
Since Turing Machine implementations of functions will vary, and one is often most interested in the underlying function that
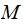 implements we
are usually interested in
implements we
are usually interested in
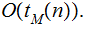
In fact, a typical application speaks to the existence of a Turing Machine
implementation,
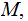 of a given function such that
of a given function such that
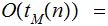 constant
time, linear time, polynomial time , logarithmic time , exponential,
time.
constant
time, linear time, polynomial time , logarithmic time , exponential,
time.
Two Examples:
1.
Thinking of the following polynomials as two Turing Machine implementations of the same function:
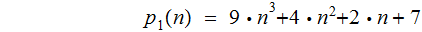
 8
multiplications and 3 additions.
8
multiplications and 3 additions.
also
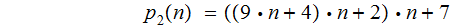
 3
multiplications and 3 additions. (Horner's Method)
3
multiplications and 3 additions. (Horner's Method)
But
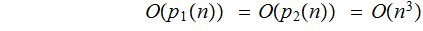
However, In discussing the complexity of the underlying
function we are interested Horner's Method, in particular
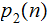 :
:
2.
Towers of Hanoi Revisited- 5 Disk Output:
1AB2AC1BC3AB1CA2CB1AB4AC1BC2BA1CA3BC1AB2AC1BC5AB1CA2CB1AB3CA1BC2BA1CA4CB1AB2AC1BC3AB1CA2CB1AB
The Pegs:
A-B A-C B-C A-B
C-A C-B A-B A-C B-C B-A C-A B-C
A-B A-C B-C A-B C-A C-B
A-B C-A B-C B-A C-A C-B A-B A-C B-C
A-B C-A C-B A-B
The Disks:
1213121412131215121312141213121
Given a Turing
Machine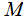 that halts on all inputs, the space complexity of
that halts on all inputs, the space complexity of
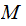 is
the function
is
the function
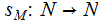
where:
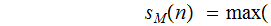 number
of cells scanned such that
number
of cells scanned such that
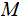 halts
on an input of length
halts
on an input of length
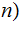
The largest number of tape cells a Turing machine visits on all inputs of a given length
How much memory is required to do a calculation where the input is of a given size
Given a Universal Turing
Machine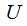 there
will be different Turing Machines implementation strings
there
will be different Turing Machines implementation strings
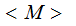 that produce.a
given
output.
that produce.a
given
output.
Provisional Definition: For a given output string
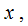 let
let
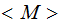 be
an input string for
be
an input string for
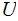 ,
such that
,
such that
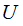 halts
with
halts
with
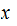 on
the tape
on
the tape
Descriptive or Kolmogorov Complexity
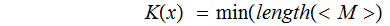 all
all
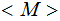 that
halt with
that
halt with
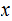 on
the
tape.
on
the
tape. 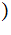
Notes:
There is a constant
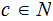 such that for all
such that for all
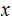
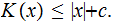
Just choose
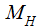 such
that it halts as soon as it starts basically one instruction:
such
that it halts as soon as it starts basically one instruction:
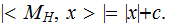
The Towers of Hanoi and Huffman Coding ;