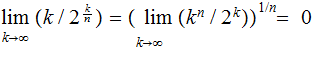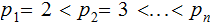 be the finite list of primes. . Let
be the finite list of primes. . Let
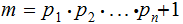 Clearly none of the primes in the list divide
Clearly none of the primes in the list divide
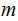 But by elementary number theory there must be primes that divide
But by elementary number theory there must be primes that divide
"The fundamental problem of communication is that of reproducing at one point either exactly or
approximately a message selected at another point. Frequently the messages have meaning; that
is they refer to or are correlated according to some system with certain physical or conceptual
entities. These semantic aspects of communication are irrelevant to the engineering problem.
The significant aspect is that the actual message is one selected from a set of possible messages.
The system must be designed to operate for each possible selection, not just the one which will
actually be chosen since this is unknown at the time of
design."
Claude Shannon
The mathematical theory of
communication.(1948)
"Our definition of the quantity of information has the advantage that it refers to individual objects
and not to objects treated as members of a set of objects with a probability distribution given
on it. The probabilistic definition can be convincingly applied to the information contained, for
example, in a stream of congratulatory telegrams. But it would not be clear how to apply it, for
example, to an estimate of the quantity of information contained in a novel or in the translation
of a novel into another language relative to the original. I think that the new definition is capable
of introducing in similar applications of the theory at least
clarity of principle.".
Andrey. Kolmogorov.
Combinatorial foundations of information theory and the calculus of
probabilities.(1983)
"The word `information' has been given different meanings by
various writers in the general field of information theory. It is likely that
at least a number of these will prove sufficiently useful in certain
applications to deserve further study and permanent recognition. It is hardly
to be expected that a single concept of information would satisfactorily
account for the numerous possible applications of this general
field."
Claude Shannon
(1993?)
The Pitcher and the Pitching Coach:
While the game is going on, which the pitcher is on the mound A pitcher and pitching communicate in two ways.
Using Shannon Information Theory - Hand signals, which work because of a common semantic content set.
Using Kolmogorov Information Theory - Trips to the mound by the pitching coach which have to be brief because of the umpire but require the transfer of semantic content, how to pitch to the next batter that had not be previously discussed.
Theorem:
There are an infinite number of primes:
Proofs:
Euclid:
Suppose not, let
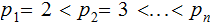 be the finite list of primes. . Let
be the finite list of primes. . Let
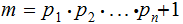 Clearly none of the primes in the list divide
Clearly none of the primes in the list divide
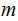 But by elementary number theory there must be primes that divide
But by elementary number theory there must be primes that divide
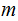 , not on the list.
, not on the list.
An Encoding Argument:
A simple case:
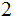 is not the only prime:
is not the only prime:
Suppose it were, then every number is of the form
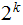 .
There are
.
There are
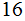 numbers in
numbers in
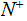
 less
than or equal to
less
than or equal to
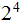 but
only
but
only
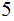 of the form
of the form
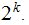
In general:
Suppose
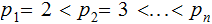 is the finite list of primes.
is the finite list of primes.
Suppose every
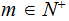 can be written in the form
can be written in the form
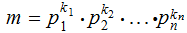 ,
let
,
let
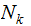 be
the set of integers in
be
the set of integers in
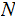 such that
such that
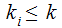 for
all
for
all
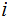 .
.
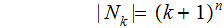
Next, let
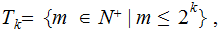
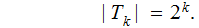
And

since, given that
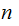 exists( there are only
exists( there are only
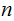 primes), any
primes), any
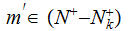 has
at least one
has
at least one
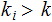 so
so
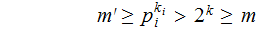 .
for
.
for
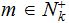 .
.
Completing the proof amounts to showing that for large enough
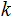 ,
,
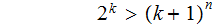
Hence,
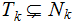 contradicting the hypothesis
contradicting the hypothesis
To show that for large
enough ,
,
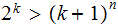 it suffices to show:
it suffices to show:
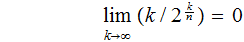
a fairly straight forward limit
argument.
Some details:
Since
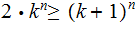 it suffices to show
it suffices to show

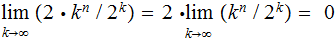
Finally it suffices to show