 and
say that this looks what I should have gotten.
and
say that this looks what I should have gotten.
Perhaps a good point of view of the role of this chapter is
to consider Kolmogorov complexity as a way of thinking.
Element of Information Theory, Second Edition,
Thomas M. Cover and Joy A. Thomas
. The theory [Quantum Mechanics] says a lot, but does not really bring us any closer to the secret of the "old one."
I, at any rate, am convinced that He does not throw dice.
A. Einstein
As science developed from antiquity to the present, it was recurrently faced with the question of thether nature is subject to chance to any extent, or evolved deterministically.
For most of that time the need to include chance was avoided by abstraction: the subject of study was so delimited as to allow its description as a deterministically evolving system.
As the theory of probability developed in modern times even chance came within the fold of predicability,
and the degree of abstraction could be lowered.
Chapter 2 Determinism
Quantum Mechanics, An Empiricist View
Bas C. Van Frassssen
In short, our gentleman became so immersed in his reading that he spent whole nights from sundown to sunup
and his days from dawn to dusk in poring over his books, until,
finally, from so little sleeping and so much reading, his brain dried up and he went completely out of his mind..
Don Quixote
Miguel de Cervantes
The Standard Example: Sitting with a friend , you flip a coin
100 times and get a Head every time. You claim that something is wrong with
the coin. Your friend asks you why you said that. You show a sequence of a mix
of 100 Heads and Tails
 and
say that this looks what I should have gotten.
and
say that this looks what I should have gotten.
"What is the probability of what you got?" , asks your friend.
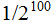 you say. "And the probability of getting what you showed me?"
"
you say. "And the probability of getting what you showed me?"
"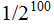 "
you say
"
you say
"And what's the problem with the coin?" ,your friend asks..
The Definition of a Probability Measure Revisited.:
Suppose we are given a set
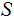 and
and
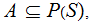 a Sigma Algebra, a Probability Measure on
a Sigma Algebra, a Probability Measure on
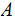 is a function
is a function
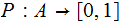 such that
such that

If
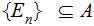 is a countable (again could be finite) subset such that
is a countable (again could be finite) subset such that
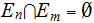 for
for
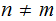 then
then
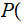
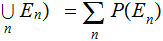
In the context of Probability, we will call
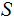 the Sample Space.
the Sample Space.
The Usual Example:
Let
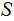 be a finite set and
be a finite set and
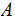 a Sigma Algebra on
a Sigma Algebra on
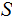 .
For any
.
For any
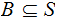 let
let
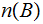 be
the number of members in
be
the number of members in
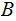 ,
then
,
then
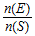 for
all
for
all
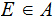 is a Probability Measure on
is a Probability Measure on
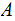 .
.
DEFINITION:
Given a set
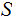 ,
a Sigma Algebra
,
a Sigma Algebra
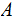 on
on 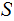 ,
and a countable discrete set
,
and a countable discrete set
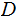 ,
a Discrete Random Variable is a function
,
a Discrete Random Variable is a function
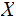
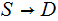 such that if
such that if
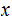 is in the image of
is in the image of
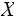 then
then
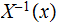 is in
is in
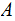 .
.
If
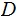 ,
is finite then we will call
,
is finite then we will call
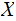 a Finite Random
Variable.
a Finite Random
Variable.
We
write
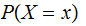 for
for
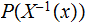
In the setting of 1. , if
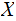 is a Finite Random Variable then
is a Finite Random Variable then
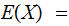
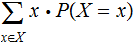
The Really Super Computer Revisited:
The programs we are now interested are those that realize 1 to 1 recursive
functions of the form
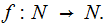 ,
,
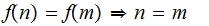
That is, if we load
 into
our computer, write
into
our computer, write
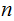 in the appropriate place in memory, and start the program, after a while the
program halts and we find
in the appropriate place in memory, and start the program, after a while the
program halts and we find
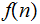 in the appropriate place in memory.
in the appropriate place in memory.
The Program
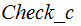 -
This program accepts as input a Natural Number and returns
-
This program accepts as input a Natural Number and returns
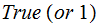 if
is one of our target programs and
if
is one of our target programs and
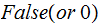 if it is not. Again everything is to be thought of as taking place in
The Computer. We will write
if it is not. Again everything is to be thought of as taking place in
The Computer. We will write
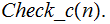 (We should to verify that
(We should to verify that
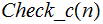 still
can't be written but that is not relevant this discussion about Kolmogorov
Complexity )
still
can't be written but that is not relevant this discussion about Kolmogorov
Complexity )
The Program
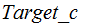 -
This program accepts as input a Natural Number
-
This program accepts as input a Natural Number
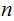 and returns the number
and returns the number
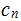 ,
the internal representation, of the
,
the internal representation, of the
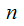 th
Target Program. We write
th
Target Program. We write
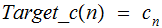
The Really Super Computer is now in a position to compute the corresponding
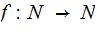
Really Random Sequences:
A definition for this
discussion: A
( not necessarily anything )
function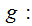
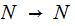 is
called really random If for any 1-1 recursive
is
called really random If for any 1-1 recursive
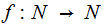
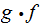 is
not recursive.
is
not recursive.
A definition for this
discussion: A
( not necessarily anything )
function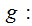
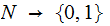 is
called really probabilistic
is
called really probabilistic
if, letting
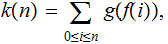 If
there is a number
If
there is a number
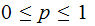 such
that for any 1-1 recursive
such
that for any 1-1 recursive
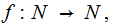
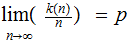
The Questions:
Is really probabilistic really random? For
 or
or
 .
For
.
For 
Is a really random
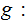
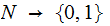 really
probabilistic?
really
probabilistic?
The Roulette Wheel , the Cell Phone, and the Winner's App:


The App can:
Calculate the velocity and acceleration of the ball in real time.
Calculate the velocity acceleration of the wheel in real time.
Predict the number that the will contain the
ball.
Setting:
Unless otherwise stated, below the term "string" is
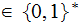 ,
a string of
,
a string of
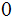 s
and
s
and
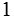 s.
s.
Definition:
Given a Universal Turing Machine,
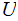 ,
the Kolmogorov Complexity,
,
the Kolmogorov Complexity,
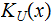 of
a string
of
a string
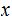 is defined to the the length of the shortest program
is defined to the the length of the shortest program
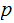 that prints
that prints
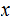 and halts.
and halts.
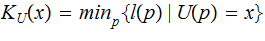
The following definitions, for Universal Prefix Turing Machines will be particularly relevent to the next lecture :
Prefix Kolmogorov Complexity is defined as the shortest
program
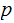 , for which the Universal Prefix Turing Machine
, for which the Universal Prefix Turing Machine
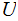 outputs
outputs 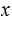
Conditional Prefix Kolmogorov Complexity: (given
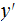 a prefix encoding of
a prefix encoding of
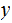 )
)
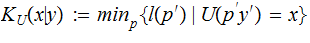
Joint Prefix Kolmogorov Complexity:
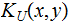
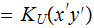
Theorem - Upper bounds:
There exists a constant
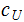 such that
such that
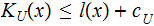
For Prefix Universal Turing
Machines 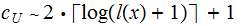 (The
Prefix Encoding prefix +a very short program)
(The
Prefix Encoding prefix +a very short program)
Proof:
The data on the input tape is
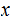 and the program is copy the data to the output tape and halt.
and the program is copy the data to the output tape and halt.
Theorem - Invariance:
Given Universal Turing Machines
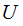 and
and
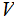 there
is a constant
.
there
is a constant
.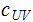 , such that for any
, such that for any
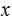 :
:
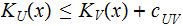
Proof:
Since
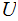 is Universal let
is Universal let
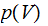 be
its emulation on
be
its emulation on
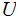 .
.
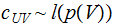 The
rest of the proof amounts to noting that any program that can be run on
The
rest of the proof amounts to noting that any program that can be run on
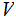 can be run on
can be run on
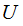 using
the emulation.
using
the emulation.
Definition:
A real -valued function
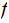
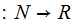 is
defined to be upper semi-computable if there is a "rational
valued" recursive function
is
defined to be upper semi-computable if there is a "rational
valued" recursive function
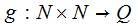 such
that:
such
that:
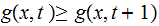
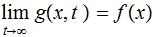
For rational valued, read a numerator recursive function and
a denominator recursive function.
Theorem - Incomputability But Upper Semi-computability
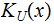 is not computable (recursive). It can be approximated from above, it is upper
semi-computable.
is not computable (recursive). It can be approximated from above, it is upper
semi-computable.
Proof:
Essentially the Halting Problem or
 There are only finitely many programs of a certain size to be looked, but you
can never be sure if they halt with the desired output. Maybe they just run
forever.
There are only finitely many programs of a certain size to be looked, but you
can never be sure if they halt with the desired output. Maybe they just run
forever.
Any finite string of 1 s and 0 s is primitive recursively enumerable.
The digits in the decimal expansion of
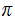 appear
to be randomly
distributed.
appear
to be randomly
distributed.
Definition:
Let
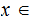
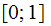 be
real number and let
be
real number and let
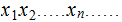
be its binary representation.
define
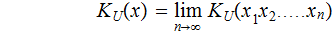
Definition:
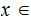
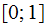 is
said to be algorithmically random if for some
is
said to be algorithmically random if for some
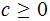
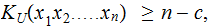 all
all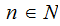
Theorem:
Randomly chosen real number are algorithmically random with probability
one.