Properties of Prefix Complexity

For nothing ought to be posited without a reason given, unless it is self-evident or known by experience or proved by the authority of Sacred Scripture.

Ockham's Razor,

William of Ockham (c. 1287--1347)

We are to admit no more causes of natural things than such as are both true and sufficient to explain their appearances

Isaac Newton(1642-1727)

Neumann's proposal to call Shannon's function defining information by the name `entropy' opened a Pandora's box of intellectual confusion.

Antoine Danchin , French geneticist

My greatest concern was what to call it. I thought of calling it `information', but the word was overly used, so I decided to call it `uncertainty'. When I discussed it with John von Neumann, he had a better idea. Von Neumann told me, `You should call it entropy, for two reasons. In the first place your uncertainty function has been used in statistical mechanics under that name, so it already has a name. In the second place, and more important, nobody knows what entropy really is, so in a debate you will always have the advantage.

A Version of A Quote that is Attributed to Claude Shannon

Information theory has, in the last few years, become something of a scientific bandwagon. Starting as a technical tool for the communication engineer, it has received an extraordinary amount of publicity in the popular as well as the scientific press. In part. this has been due to connections with such fashionable fields as computing machines, cybernetics, and automation; and in part, to the novelty of its subject matter. As a consequence, it has perhaps been ballooned to all importance beyond its actual accomplishments....... ........ In short, information theory is currently partaking a somewhat heady draught of general popularity. And although this wave of popularity is certainly pleasant and exciting for those of us working in the field, it carries at the same time all element of danger. While we feel that information theory is indeed a valuable tool in providing fundamental insights into the nature of communication problems and will continue to grow in importance, it is certainly no panacea for the communication engineer or, a fortiori, for anyone else. Seldom do more than a few of nature's secrets give way at one time. It will be all too easy for our somewhat artificial prosperity to collapse overnight when it is realized that the use of a few exciting words like information, entropy, redundancy do not solve all of our problems

Claude Shannon

...As Dr. Shannon suggests in his editorial: The Bandwagon, [InformationTheory] is beginning to suffer from the indiscriminate way in which it has been

taken as a solution of all informational problems, a sort of magic key. I am pleading in this editorial that Information Theory... return to the point of view

from which it originated: the ... statistical concept of communication.

Norbert Wiener

A Random Variable is neither Random nor a Variable.

Gian-Carlo Rota

'When I use a word,' Humpty Dumpty said, in rather a scornful tone, 'it means just what I choose it to mean --- neither more nor less.'

'The question is,' said Alice, 'whether you can make words mean so many different things.'

'The question is,' said Humpty Dumpty, 'which is to be master --- that's all.'

Through the Looking Glass

Lewis Carroll

________________________________________________________________________________

An Interesting Calculation:

________________________________________________________________________________

Setting:

Below we are only considering Universal Prefix Turing Machines

Repeating definitions from the previous lecture:

Prefix Kolmogorov Complexity is defined as the shortest prefix program 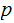$\QTR{Large}{p}$ , for which the Universal Prefix Turing Machine 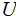$\QTR{Large}{U}$ outputs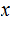

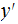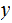Conditional Prefix Kolmogorov Complexity: (given a prefix encoding of $\QTR{Large}{y}$ )

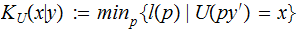
Joint Prefix Kolmogorov Complexity:

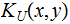
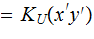
Definition:

Let 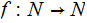be a partial recursive function, Define:

____________________________________________________________________________________

Kraft's inequality:

_____________________________________________________________________________________

algorithmically random:.

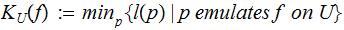
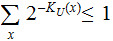
Definition:

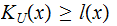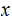If then $\QTR{Large}{x}$ is called algorithmically random.

"Most Strings are algorithmically random." There are more strings of a given size than short programs to compute them.

Real Numbers:

Any finite string of 1 s and 0 s is primitive recursively enumerable.
The digits in the decimal expansion ( the file) of 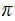$\QTR{Large}{\pi }$ appear to be randomly distributed.

Digit 0 1 2 3 4 5 6 7 8 9

Frequency 418919 419139 419163 419092 420392 419436 418413 419907 419653 420192

Probability .0998780 .09993048 .0999362 .09991927 .10022922 0.100001287 .099757385 .10011358 .100053024 .100181532

Definition:

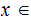
Let 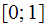$\QTR{Large}{x\in }$ be real number and let

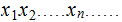
be its binary representation.

define

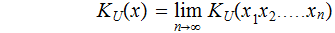
Definition:

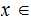
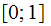$\QTR{Large}{x\in }$ is said to be algorithmically random if for some

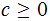
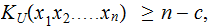all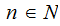

Theorem:

Randomly chosen real number are algorithmically random with probability one

_____________________________________________________________________________________

Symmetry:

_____________________________________________________________________________________

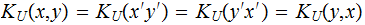
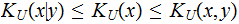
Additional Information and Subadditivity:

and

____________________________________________________________________________________

Functional Subadditivity:

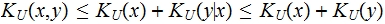
For 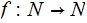partial recursive

____________________________________________________________________________________

Ockham's Razor and Kolmogorov Complexity:

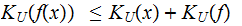
Topics for discussion:

The Ackermann Function is certainly short but is it not complex?
That a string does not admit a short description, is algorithmically random, seems to be a very reasonable measure of complexity.

Digit	0	1	2	3	4	5	6	7	8	9
Frequency	418919	419139	419163	419092	420392	419436	418413	419907	419653	420192
Probability	.0998780	.09993048	.0999362	.09991927	.10022922	0.100001287	.099757385	.10011358	.100053024	.100181532