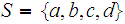Homework Assignment 3

3.2

Which of the following lists of subsets of the set 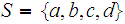form topologi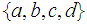es.

- - Yes

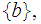
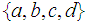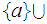
- - No 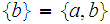not in the list.

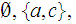
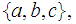
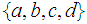- Yes

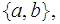
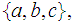
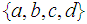- No , closed under union and intersection and 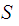$\QTR{Large}{S\ }$ is in the list, but 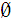is not.

3.4

Prove that a function 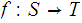is continuous if and only if the inverse image of every closed set is closed.

Proof:

We use the following equations from the Boolean algebra of sets.

If 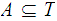is any subset. then

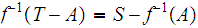
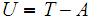
Suppose the inverse image of every closed set is closed. Let $\QTR{Large}{U}$ be an open set and $\QTR{Large}{U=T-A}$

Then $\QTR{Large}{A}$ is closed and so 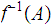is closed hence is open.

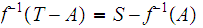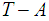Suppose that $\QTR{Large}{f}$ is continuous and $\QTR{Large}{A}$ is closed then is open since $\QTR{Large}{T-A}$ is open

but then 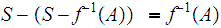is closed.

3.8

Let 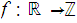be the floor function. 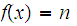for

Is $\QTR{Large}{f}$ continuous?

Answer:

No because the supspace topology on is descrete so points are open sets but

not an open set.

3.8

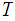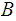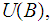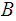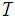Let $\QTR{Large}{T}$ be a set and $\QTR{Large}{B}$ a collection of subsets closed under finite intersection, then $\QTR{Large}{U(B),}$ the set of arbitrary unions of sets of $\QTR{Large}{B}$ form a topology.on $\QTR{Large}{T}$ [ Added : $\QTR{Large}{T}$ and 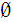are in $\QTR{Large}{B}$ ]

Proof:

Again, the solution amounts to recalling some properties of Boolean Algebras. In this case

$\QTR{Large}{\cup }$
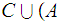
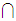
$\QTR{Large}{\cap }$
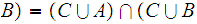
More generally, if 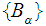and are 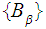indexed set of sets then

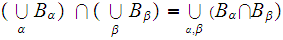
and similarly for any arbitrary collection of indexed sets.
And if and are indexed set of sets then where is either in the index set or in the index set and similarly for an arbitrary collections of index sets.

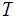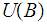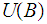We are given that $\QTR{Large}{T}$ and are in $\QTR{Large}{U(B)}$ . We are also given that arbitrary unions of sets of $\QTR{Large}{U(B)}$ is in $\QTR{Large}{U(B)}$ . This is because a union of unions of sets in $\QTR{Large}{U(B)}$ is a union of sets. That a finit intersection of sets of $\QTR{Large}{U(B)}$ is in $\QTR{Large}{U(B)}$ is because an intersection of unions of sets in 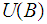$\QTR{Large}{U(B)}$ is a union of intersections of sets.