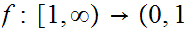
![$\QTR{Large}{]}$](graphics/Exam1aanswers__2.png) where
where
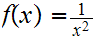 and
and
1. (20points)
Consider
the function
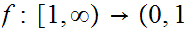
![$\QTR{Large}{]}$](graphics/Exam1aanswers__2.png) where
where
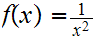 and
and
 are given the subspace topology. Show that
are given the subspace topology. Show that
 is
continuous.
is
continuous.
Solution:
From the definition of continuity, we need to show that for every
 and
and
 we can find a
we can find a
 so that if
so that if
 and
and
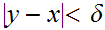
then

But,
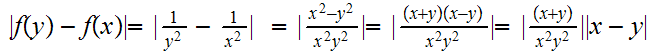
( one continuation)
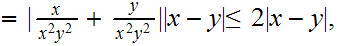 Since
Since
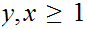
(a second continuation)
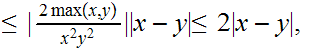 Since
Since
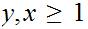
So
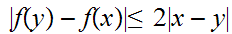 .
Choose
.
Choose
 .
.
(a third continuation)
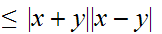 Since
Since
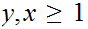
now you have to
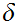 based on
based on
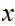 .
Assume
.
Assume
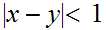 ,
then
,
then
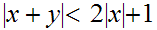
so
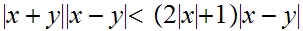 . So choose
. So choose
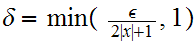 .
.
2.
a. (10 points)
Let
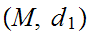 and
and
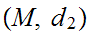 be two Metric Spaces with the same underlying set
be two Metric Spaces with the same underlying set
 .
Suppose that for every
.
Suppose that for every
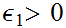 there is an
there is an
 such
that for all
such
that for all
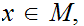
 ,
and that for every
,
and that for every
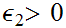 there is an
there is an
 such
that for all
such
that for all
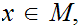
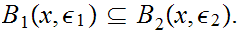 Show that
Show that
 and
and
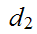 generate the same topology.
generate the same topology.
b .(20 points)
In the setting of a. , suppose that there is some
fixed real number
 such that for all
such that for all
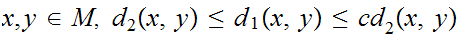 .
Show that
.
Show that
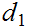 and
and
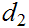 generate the same topology by giving formulae for
generate the same topology by giving formulae for
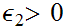 given
given
 , and
, and
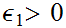 given
given
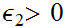 that produce the necessary set inclusions of a.
that produce the necessary set inclusions of a.
Hint:
Think of
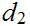 as
measuring in miles and
as
measuring in miles and
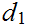 as
measuring in kilometers. If you are within
as
measuring in kilometers. If you are within
 miles of
miles of
something
then you certainly within
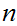 kilometers.
kilometers.
Solution:
a.
By
definition,
 be open with respect to
be open with respect to
 if
for
any
if
for
any  we can find some
we can find some
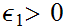 such that
such that
 .
But by assumption we can find
.
But by assumption we can find
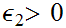 such
that
such
that
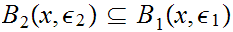 ,
and hence
,
and hence
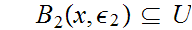 so
so
 is also open with respect to
is also open with respect to
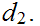 The
proof the other way is identical.
The
proof the other way is identical.
b.
First we use
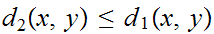 to show that
to show that

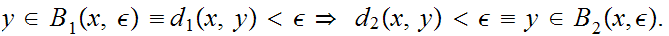
so
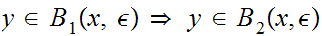 or
or
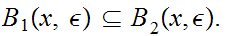
Next use
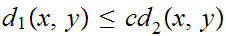 to show that
to show that
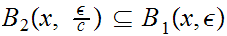
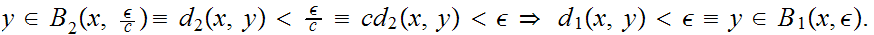
3.
a. (10 points) State the Least Upper Bound Property for the Real Numbers and use it to prove:
b.
(20 points) Let
 be
any continuous function. Show that such that
be
any continuous function. Show that such that
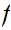 has a fixed point. That is there is
has a fixed point. That is there is
at
least one
 with
with
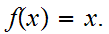
Hint: What can one say about the continuous function
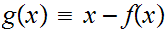 ?
?
Note:
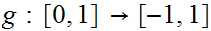
Solution:
a.
The Least Upper Bound Property states that every set of Real Numbers that has an upper bound has a least upper bound.
b.
We need to find some
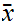 such that
such that
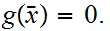 Suppose
there was no such
Suppose
there was no such
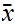 .
.
Let
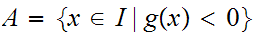 We
know that
We
know that
 and
and
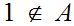 .
(
.
(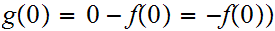
Let
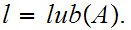 Since
Since
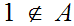 we know
we know
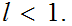 We
also know that for
We
also know that for
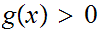 for
for

Suppose

Since
 is
continuous there exists a
is
continuous there exists a
 such
that
such
that
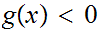 for all
for all
 contradiction the
contradiction the
previous statement.
Suppose
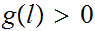 .
.
Again,
since
 is continuous there exists a
is continuous there exists a
 such
that
such
that
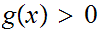 for all
for all

But since
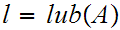 for
any
for
any
 there exists an
there exists an
 such that
such that
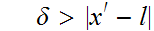 .
In particular
.
In particular
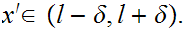 But
But
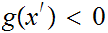 ,
again a contradiction.
,
again a contradiction.
Hence
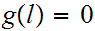 or equivalently,
or equivalently,
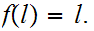
4. (20 points)
Let
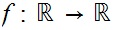 be
any continuous function. Let
be
any continuous function. Let
 be the fixed point set
be the fixed point set
 .
Prove that
.
Prove that
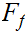 is
closed.
is
closed.
Hint:
One version of the proof shows that
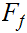 contains all its limit points,hence is closed. The informal, freshman
contains all its limit points,hence is closed. The informal, freshman
calculus version of this is:
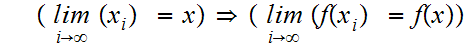 so if
so if
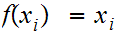 for all
for all
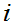 then
then
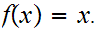
Solution:
A proof that
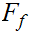 contains
all its limit points.
contains
all its limit points.
Let
 be a limit point of
be a limit point of
 , in particular for any
, in particular for any
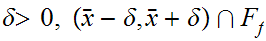
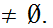
We need to show
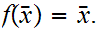 Suppose
Suppose
 and
let
and
let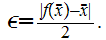 Since
Since
 is continuous choose
is continuous choose
 such that
such that
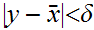
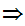
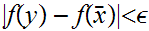 .
Since
.
Since
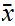 is a limit point of
is a limit point of
 we
can choose that
we
can choose that
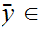
 such
that
such
that
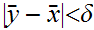 but then by the triangle inequality
but then by the triangle inequality

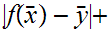
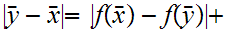

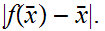
A contradiction!
A proof that shows the complement of
 is
open.
is
open.
If
 then
then
 .
Choose any
.
Choose any
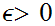 such that
such that
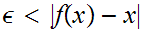 .
.
To shorten some of the formulae I will use metric space notation (
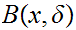 for
for
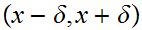 )
)
From the definition of
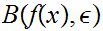 ,
,
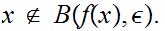
Since is continuous
 is open and contains
is open and contains
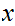 .
.
and
We can choose
 such
that
such
that

I claim

If not let
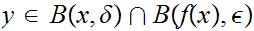 then
then
 and
and
 so
so

contradicting the definition of

But since
 this
implies that
this
implies that
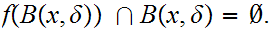
and
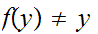 for
for
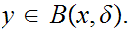
Thus
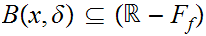 and since
and since
 is arbitrary
is arbitrary
 is
open.
is
open.