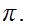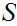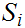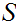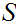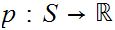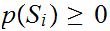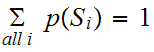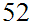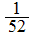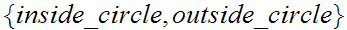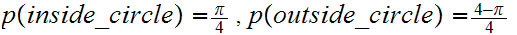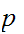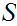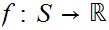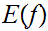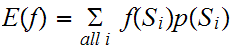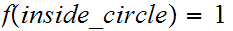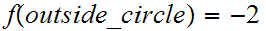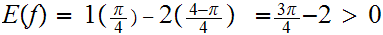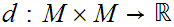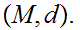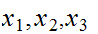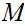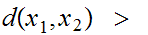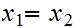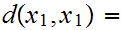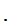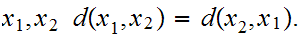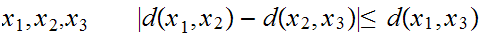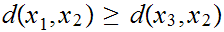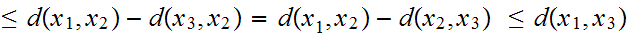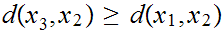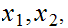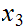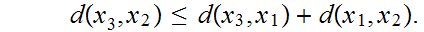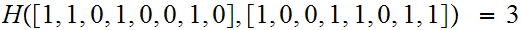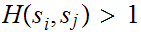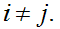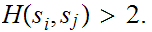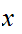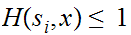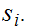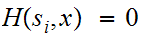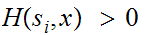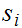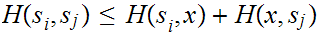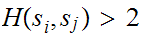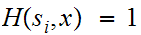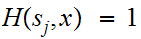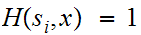Topics in The Theory of Computation
Probability
- A very short course:
A Probabalistic Computer:
-
Take two urns, each containing
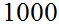 balls of identical size,
labled
balls of identical size,
labled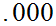 to
to
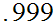 .
Perform the following computation:
.
Perform the following computation:
-
Without looking, select one ball from each urn. We denote them by their lables
"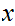 "
and
"
"
and
"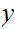 ".
".
-
Compute
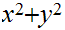 , record the result, and put the balls back into their urns.
, record the result, and put the balls back into their urns.
-
Repeat 1. 2. 3. a few hundred times.
-
Count the number of times that
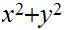
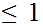 .Multiply
this number by
.Multiply
this number by
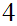 .
The result is an approximation to
.
The result is an approximation to
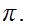
Why?
Terminology :
Suppose we have an experiment with a finite number of possible outcomes, all
of which depends on chance.
-
The sample space of the experiment is the set of all possible
outcomes.In general we will use the letter
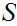 to denote such a set and
to denote such a set and
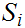 to denote members of
to denote members of
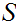 .
.
-
A probability distribution (or just
distribution ) on
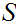 is a real valued function
is a real valued function
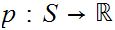 such that
such that
Examples:
Expected Value:
Suppose we are given a a distribution
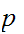 on
on
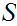 and a function
and a function
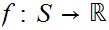 . The expected value
. The expected value
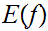 is defined by the formula
is defined by the formula
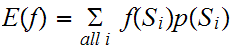
Example:
In the second example above, suppose
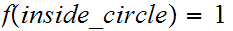 and
and
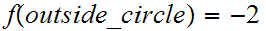
then
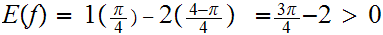
______________________________________________________
Metric
Spaces - A very short course.
Definition:
We can abstract the notion of Euclidian Distance as follows
A Metric Space is a set
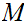 and a function
and a function
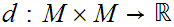 .
We write
.
We write
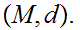
such that for all
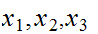 in
in
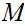 :
:
-
Positivity:
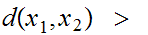 0
unless
0
unless
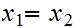 in which case
in which case
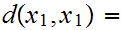 0
0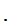
-
Symmetry: For all
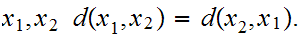
-
Triangle Inequality: For all
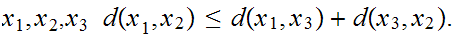
Lemma:
The the Triangle Inequality has a second, equivalent form:
For all
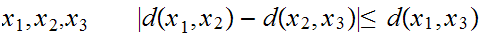
Proof:
Assume for the moment that
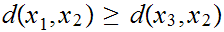 . The Triangle Inequality as written implies
. The Triangle Inequality as written implies
 0
0
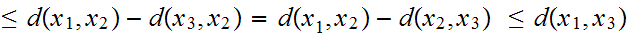
If
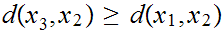
then, since the Triangle Inequality is symetric in
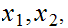 and
and
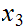 rewrite
it as:
rewrite
it as:
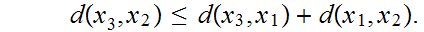
_____________________________
Hamming Distance for Bytes - An Example from
Computer Science:
Definition:
The Hamming distance between two bytes is defined to be the count of the
number of positions in which the corresponding bits differ.
For example:
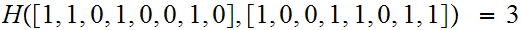
Error Detecting Codes:
Suppose we transmitting a byte code with an acceptably low probability of more
than a single bit being in error.
A code is said to be error detecting if
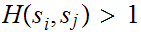 for
for
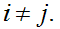
It is called error correcting if
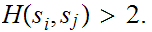
Analysis:
Our assumption that we can assume that the transmission has at most one bit in
error translates to the assumption that if we see a byte
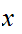 then
then
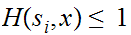 for
some
for
some
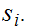 If
If
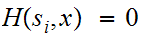 then
we can assume that that is the correct character. If
then
we can assume that that is the correct character. If
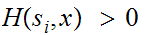 for
all
for
all
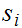 then we can assume that there is an error.
then we can assume that there is an error.
Note that since
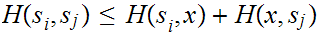 if
if
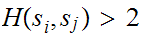 then
we cannot have
then
we cannot have
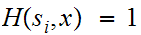 and
and
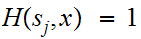
simultaneously. So if, say
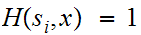 we can assume that
we can assume that
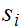 is the actual byte that was transmitted.
is the actual byte that was transmitted.
ascii
_________________________________________________
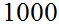 balls of identical size,
labled
balls of identical size,
labled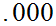 to
to
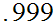 .
Perform the following computation:
.
Perform the following computation:
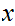 "
and
"
"
and
"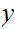 ".
".
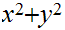 , record the result, and put the balls back into their urns.
, record the result, and put the balls back into their urns.
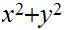
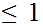 .Multiply
this number by
.Multiply
this number by
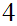 .
The result is an approximation to
.
The result is an approximation to