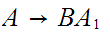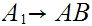Review for Mid-Term

From the Notes on Ambiguity (13)

HW Due Sept 29: Are Context Free Grammars sufficent to capture the usual precedence rules for 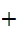$\QTR{Large}{+\ }$ and $\QTR{Large}{\ast }$ without ambiguity?

____________________________________________________________________________________

From the Proof of the CFLPumpingLemma (15)

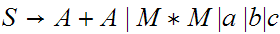
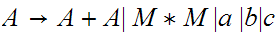
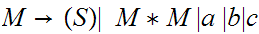
Since G is in Chomsky Normal Form the tree looks like .

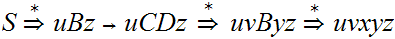With eithe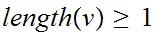r or 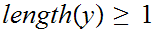(or both). (Home Work Due Sept 29: How could one be zero?)

But then, by substituting ,

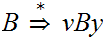(Home Work Due Sept 29: How could we choose B so as to guarantee 3. in the statement of the Theorem? Note that we do not use this in our applications)

See The Proof

___________________________________________________________________

From the Text:

Page 88 Problem 1.25

The strings are

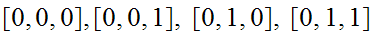
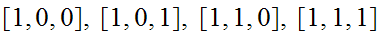
the states are

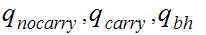where represents an invalid binary addition.

The start state is

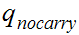
The only accepting state is 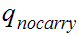. If we reach it at the end of the string it means that there is no carry hence the binary addition is correct.

Finally

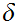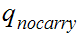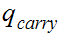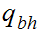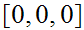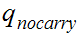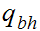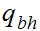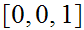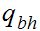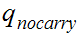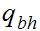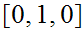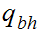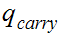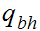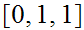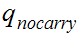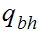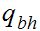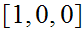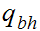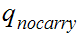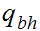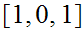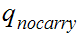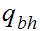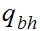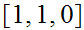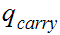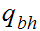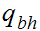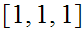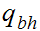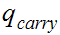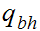where

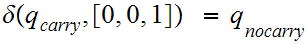reads

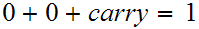
and

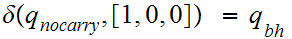reads 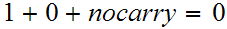is not a valid binary add.

Page 129 Problems 2.8 ,

the girl touches the boy with the flower

__________________________________________

2.9

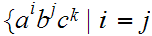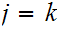Show or $\QTR{Large}{j=k}$ where 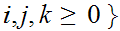is a CFL.

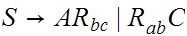
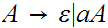
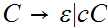
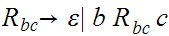
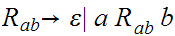
The language is ambiguous. Look at strings of the form

___________________________________________

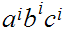
2.14

Convert to Chomsky Normal Form.

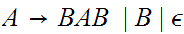
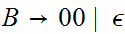
I am assuming that 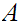$\QTR{Large}{A}$ is the starting state.

Add a new starting state.
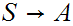
Remove rules 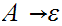and
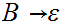
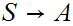
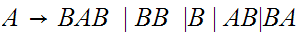
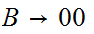
Remove
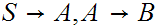
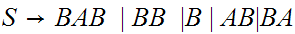
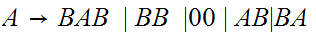
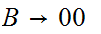
Remove terminals from strings of length
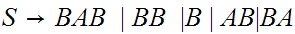
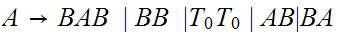
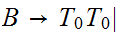
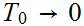
Shorten long production strings.

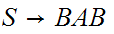becomes

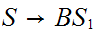
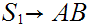
and

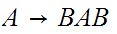becomes