
Peano's Postulates, Hilbert's Program, Godel's Theorem, and the Church - Turing Thesis

 |
Peano's Postulates, Hilbert's Program, Godel's Theorem, and the Church - Turing Thesis
|  |
The Natural numbers,
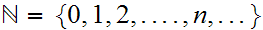 are characterized as follows:
are characterized as follows:
There is a distinguished member
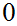 and a function
and a function
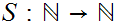 with the following properties:
with the following properties:
(P1) There is no Natural number
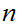 such that
such that
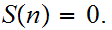
(P2) For all
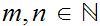 if
if
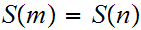 then
then
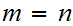
(P3) Mathematical Induction for the Natural Numbers :
Suppose that we have a proposition
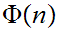 on
on
 .
Suppose
.
Suppose
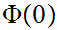 is true and
is true and
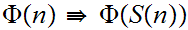 is true for all
is true for all
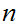 .
Then,
.
Then,
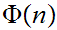 is true for all
is true for all
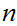 .
.
Note: We sometimes write
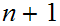 for
for
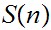 )
)
__________________________________________________
The Definition of Addition:
We define a function
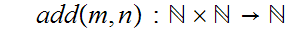
"inductively" as follows:
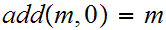 read
read
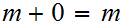
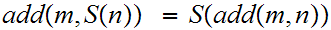 read
read
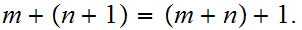
______________________________________________
The Definition of Multiplication:
We define
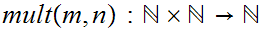
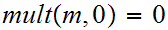 read
read
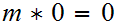
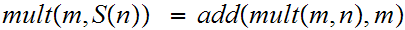 read
read
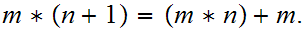
_______________________________________________
The Definition of Exponentiation: (HomeWork Due Oct
20 ) Define
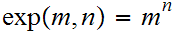
__________________________________________________________________
Theorem: Suppose we are given
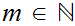 and a function
and a function
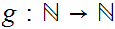 then there is a unique well defined function
then there is a unique well defined function
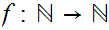 such that
such that
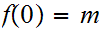
and
for all
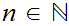
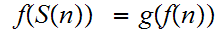 .
.
__________________________________________________________________
In the early part of the 20th Century, there was the belief amongst mathematicians that all of mathematics could be reduced to a set of complete, consistent theories. Finding these "theories" was the aim of Hilbert's Program.
Informally, a "theory" is a set of assumed statements (Axioms) and a set of
rules of deduction, which allow us to deduce a set of additional statements( Theorems).
Underlying a theory is a "model." For example, the Natural Numbers would be the model for Peano's Postulates.
We might ask if Peano's Postulates are "complete," can all true statements about the Natural Numbers be derived from these Postulates?
We might ask if Peano's Postulates are "consistent," we cannot prove a contradiction from them.
One goal of Hilbert's Program was to show that ordinary arithmetic had a complete, consistant theory.
For any theory in which a sufficiently rich set arithmetical facts are provable, it is possible to construct arithmetical statements which, if the theory is consistent, are true but neither in the theory.
In particular, given certain technical qualifications, if you add such statements as new axioms, there will still be others that are neither provable nor refutable.
The Church-Turing thesis concerns the notion of an effective or mechanical
method in logic and mathematics. A method, or procedure,
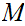 ,
for achieving some desired result is called `effective' or `mechanical' if:
,
for achieving some desired result is called `effective' or `mechanical' if:
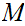 is set out in terms of a finite number of exact instructions (each instruction
being expressed by means of a finite number of symbols);
is set out in terms of a finite number of exact instructions (each instruction
being expressed by means of a finite number of symbols);
 will, if carried out without error, produce the desired result in a finite
number of steps;
will, if carried out without error, produce the desired result in a finite
number of steps;
 can (in practice or in principle) be carried out by a human being unaided by
any machinery save paper and pencil;
can (in practice or in principle) be carried out by a human being unaided by
any machinery save paper and pencil;
 demands no insight or ingenuity on the part of the human being carrying it
out.
demands no insight or ingenuity on the part of the human being carrying it
out.
Turing's thesis:
[Turing machines] can do anything that could be described as "rule of thumb" or "purely mechanical."
Church's thesis:
A function of positive integers is effectively calculable only if recursive.
We will explore the relationship between Godel's Theorem and the Church - Turing Thesis later in the semester.