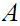 is a context-free language. There is a number
is a context-free language. There is a number
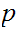 such that if
such that if
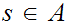 and
and
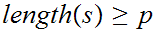
Let
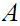 is a context-free language. There is a number
is a context-free language. There is a number
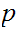 such that if
such that if
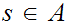 and
and
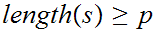
then
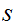 can be written as a concatination of strings
can be written as a concatination of strings
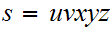 such that
such that
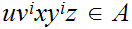 for
for
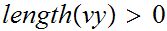
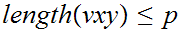
Proof:
Let
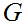 be a grammar in Chomsky Normal Form generating
be a grammar in Chomsky Normal Form generating
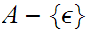 .
.
By induction on the length of path, Any parse tree generated from
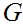 whose longest path is of length
whose longest path is of length
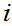 can recognize a string of length at most
can recognize a string of length at most
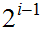 .
.
In brief:
Since the two possible forms that a production can take are
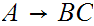 and
and
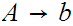 . A path in a "Chomsky Tree" is determined by a series of "left-right" choices
follow by a selection of a terminal. Hence, if the longest path is of length
. A path in a "Chomsky Tree" is determined by a series of "left-right" choices
follow by a selection of a terminal. Hence, if the longest path is of length
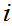 the path is uniquely determined by
the path is uniquely determined by
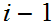 left-right choices hence there are at
most
left-right choices hence there are at
most 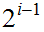 paths:
paths:
In more detail:
If
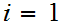 then since
then since
 is in Chomsky Normal Form, the tree has the form
is in Chomsky Normal Form, the tree has the form
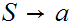 , where
, where
 is terminal. So the longest string that it can recognize is of length
is terminal. So the longest string that it can recognize is of length
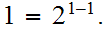
Suppone we know the result for
 and suppose the parse tree
and suppose the parse tree
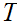 has longest path has length
has longest path has length
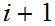 .
Then, again since
.
Then, again since
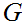 is in Chomsky Normal Form, the top of
is in Chomsky Normal Form, the top of
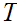 is of the form
is of the form
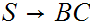 where
where
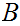 and
and
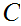 are non-terminals and
are non-terminals and
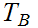 and
and
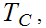 the
parts of
the
parts of
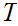 under
under
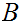 and
and
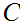 , have no path of length greater than i. Hence, by hypothesis each subtree,
, have no path of length greater than i. Hence, by hypothesis each subtree,
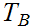 and
and
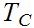 ,
can recognize a string of length at most
,
can recognize a string of length at most
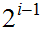 .
Thus
.
Thus
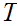 can recognize a string of length at most
can recognize a string of length at most
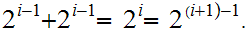
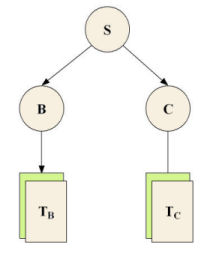
Next, assume that
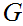 has
has
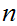 nonterminals and pick a string
nonterminals and pick a string
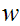 in
in
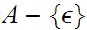 such that
such that
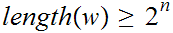 .
From the argument above, any parse tree for
.
From the argument above, any parse tree for
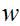 must contain a path of length greater than
must contain a path of length greater than
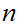 .
It follows that at least one nonterminal
.
It follows that at least one nonterminal
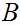 must occur at least twice on this path. In particular, since
must occur at least twice on this path. In particular, since
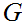 is in Chomsky Normal Form the derivation represented by the tree can be
summarized as
is in Chomsky Normal Form the derivation represented by the tree can be
summarized as
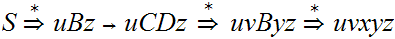 , where
, where
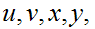 and,
and,
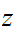 are
strings of terminals. Moreover, since the selected second occurrence of
are
strings of terminals. Moreover, since the selected second occurrence of
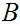 is under
is under
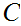 or
or
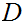 in the tree, either
in the tree, either
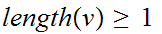 if
it is under
if
it is under
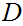 and
and
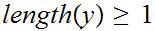 if it is under
if it is under
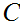 .
.
Note that since
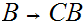 or
or
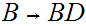 are possible production rules, it may be the case that
are possible production rules, it may be the case that
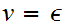 or
or
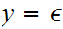 .
.
To complete this part of the argument, by substituting
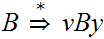 for
the second occurrence of
for
the second occurrence of
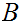 in the original tree.
in the original tree.
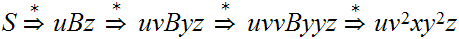 .
is also a parse tree, and, by repeated substitution, we obtain a parse tree
for
.
is also a parse tree, and, by repeated substitution, we obtain a parse tree
for
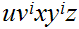 and
and
 .
.
To prove 3. , first note that
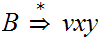 where
where
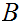 is the first occurence in the repeating pair. The result now follows from a
judicious choice of the pair of repeating non-terminals. In particular,
amongst the repeating pairs of non-terminals, choose one whose first
occurrence has the shortest path from it to the furthest leaf under it. Of
course there may be more than one. The length of path from
is the first occurence in the repeating pair. The result now follows from a
judicious choice of the pair of repeating non-terminals. In particular,
amongst the repeating pairs of non-terminals, choose one whose first
occurrence has the shortest path from it to the furthest leaf under it. Of
course there may be more than one. The length of path from
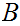 to that leaf must be less than or equal to the number of non-terminals, that
is
to that leaf must be less than or equal to the number of non-terminals, that
is
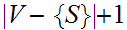 for the second occurrence of
for the second occurrence of
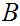 or else we could find a repeating pair with a shorter defining path.
3. now follows from what is essentially a restatement
of the initial arguments of this proof, regarding the length of paths in a
tree and the length of strings that can be recognized.
or else we could find a repeating pair with a shorter defining path.
3. now follows from what is essentially a restatement
of the initial arguments of this proof, regarding the length of paths in a
tree and the length of strings that can be recognized.
Example :
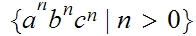 is not a CFL.
is not a CFL.
The proof is by contradiction. Suppose
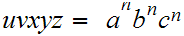 . Neither
. Neither
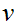 nor
nor
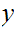 can be a mix of
can be a mix of
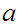 s
,
s
,
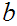 s , and/or
s , and/or
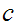 s
. To see this, suppose, for example,
s
. To see this, suppose, for example,
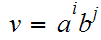 ,
then
,
then
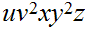 contains the sequence
contains the sequence
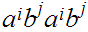 and hence
and hence
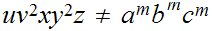 for any
for any
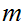 .
Next, suppose for example,
.
Next, suppose for example,
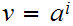 and
and
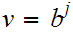 then
then
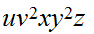 cannot
have the same number of
cannot
have the same number of
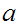 s
,
s
,
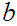 s , and
s , and
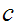 s.
s.