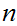 with the string
"S
with the string
"S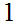 S
S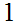 S
S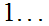 S
S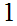 "
(the concatination of
"
(the concatination of
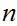 symbols
S
symbols
S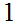 )
.
)
.
In order to avoid some set-theoretic difficulties, we identify the the "class" of Turing Machines with the set of TPL programs.
We also identifying a natural number
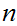 with the string
"S
with the string
"S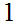 S
S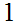 S
S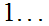 S
S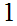 "
(the concatination of
"
(the concatination of
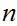 symbols
S
symbols
S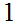 )
.
)
.
We can identify each subset
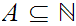 with a set of strings in one symbol,
"S
with a set of strings in one symbol,
"S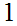 " .
We use
" .
We use
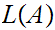 to denote this language.
to denote this language.
Recalling that
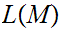 denotes
the language accepted by the Turing Machine
denotes
the language accepted by the Turing Machine
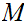 , the set of languages,
, the set of languages,
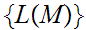 is countable. In particular, we can define a one to one map
is countable. In particular, we can define a one to one map
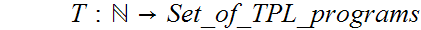
Do a Recursive search through all possible strings in TPL symbols and Recursively Enumerate all strings that are accepted as TPL programs.
There exists a subset
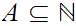 such that there does not exist a Turing Machine
such that there does not exist a Turing Machine
 with
with
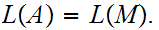 There are languages that are not accepted by Turing machines.
There are languages that are not accepted by Turing machines.
Almost by definition, the set of languages ,
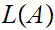 , is in one to one correspondence with the set
, is in one to one correspondence with the set
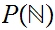 ,
but by the lemma above the set of languages ,
,
but by the lemma above the set of languages ,
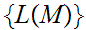 , is in one to one correspondence with
, is in one to one correspondence with
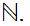 and,
from the previous section there is no onto map
and,
from the previous section there is no onto map
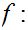 .
.
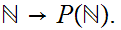
There is no Turing Machine
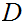 such that
such that
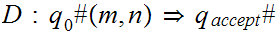 S
S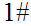 if Turing Machine
if Turing Machine
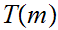 halts on input
halts on input
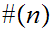
and
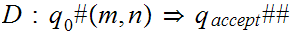 if Turing Machine
if Turing Machine
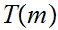 loops on input
loops on input
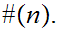
Consider the Turing Machine
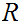 defined by the following transitions:
defined by the following transitions:
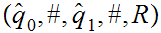
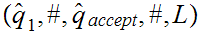
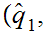 S
S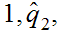 S
S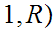
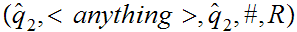
Now consider, the Turing Machine
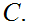 Where
Where
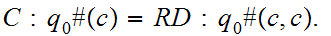 Suppose
Suppose
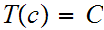 ,
we want to compute
,
we want to compute
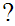 where
where
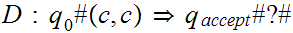
Suppose
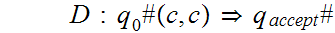 S
S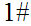
That is
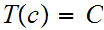 halts on input
halts on input
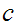 .
Then
.
Then
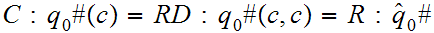 S
S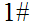 loops on input
loops on input
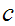 .
Remember
.
Remember
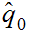 is identified with
is identified with
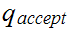 in
in
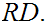
Suppose
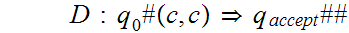
That is
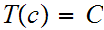 loops on input
loops on input
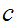 .
Then
.
Then
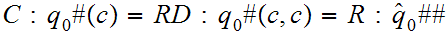 halts on input
halts on input
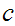 .
.