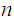by a string of
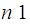s.
We represent a sequence of
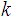natural numbers
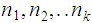by a string of the form
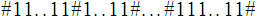where
there are
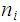
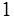s
between the
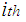and
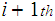
We will use the notation
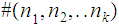to represent this string. For example,
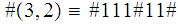
We represent a natural number
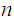by a string of
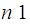s.
We represent a sequence of
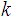natural numbers
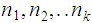by a string of the form
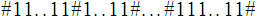where
there are
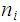
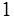s
between the
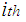and
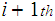
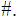We will use the notation
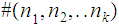to represent this string. For example,
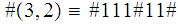
A function
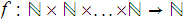,of
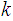variables, is called Turing Computable if there exists a
Turing Machine
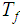
such that for all
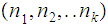we have the derivation
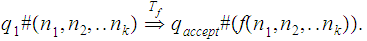
Example: Suppose
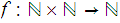
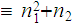
then
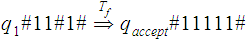
1. The successor function
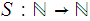is Turing Computable:
Assuming that the input tape is as above, one can easily define
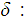
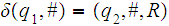
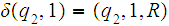
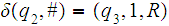
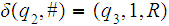
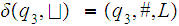
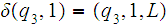
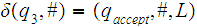
2. The projection functions
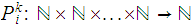are Turing Computable.
Homework: Due November 17 :
Show that
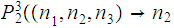is Turing Computable.
3. The set of Turing Computable functions is closed under composition.
For simplicity we consider the case of two functions of a single variable.
Assume
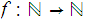and
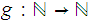are Turing Computable by Turing Machines
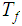
and
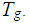We
need to produce a Turing Machine
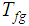that computes
.
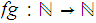By selecting alternative members, we can assume that the set of states of
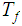
and
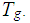are
disjoint. We let
.
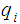denote a generic state of
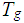and
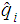denote a generic state of
.
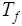With some addition bookkeeping the work is to construct an appropriate
transition function. We start with the union of the two sets of 5-tuples.
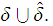Next replace all occurrences of
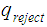with
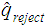. Finally, replace all occurrences of
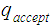with
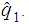Derivations have the form
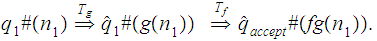
A function is recursive iff it Turing Computable. With appropriate modifications of the relevant definitions, this also holds for partial recursive functions.