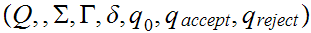 ,
where
,
where
A (PDA) is a 7-tuple
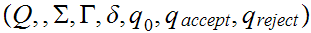 ,
where
,
where
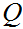 is a finite set called the states,
is a finite set called the states,
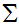 is a finite set called the input alphabet,
is a finite set called the input alphabet,
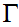 is a finite set called the tape alphabet, where
is a finite set called the tape alphabet, where
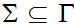 and
and
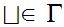 .
.
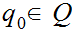 is the start
state,
is the start
state,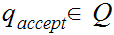 is the accept state,
is the accept state,
and
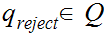 is the reject state.
is the reject state.
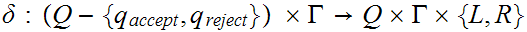 is the transition function.
is the transition function.
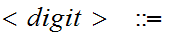 0
0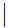 1
1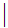 ....
....
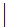 8
8
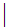 9
9
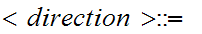 L
L R
R
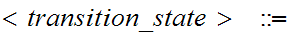 Q
Q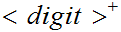
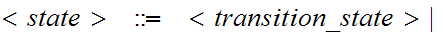 Qaccept
Qaccept Qreject
Qreject
//read the letter Q followed by one or more digits or "accept", or "reject."
//We
will use the
"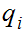 " to
denote a "transition
state."
" to
denote a "transition
state."
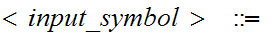 S
S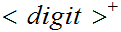
//We
will use the
"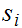 "
to denote an "input symbol."
"
to denote an "input symbol."
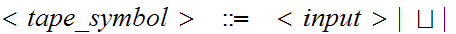 X
X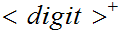
//We
will use the
"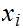 "
to denote a "tape symbol".
"
to denote a "tape symbol".
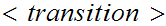
 (
(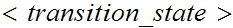 ,
,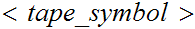 ,
,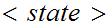 ,
,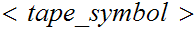 ,
,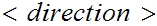 )
)
//We
will use the
"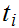 "
to denote a "transition".
"
to denote a "transition".
A TPL Program consists of:
A finite set of transition states, including Q0
, Qaccept
Qaccept ,
and Qreject .
,
and Qreject .
A finite set of tape symbols , including
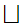
The directions L and R.
A finite set of transitions statisfying the Turing Machine transition function condition with respect to 1. and 2. .
All TPL Programs can be written using the 21 symbols
0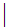 1
1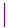 ....
....
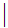 8
8
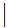 9
9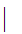 Q
Q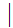 Qaccept
Qaccept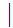 Qreject
Qreject
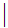 S
S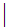
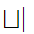 X
X
 (
(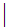 ,
, )
)
 L
L
 R
R
The Validity of a TPL Program can be decided.
States, tape_symbols, and transitions can be checked by a DFA.
That the transitions provide a transition function can be checked by a search on all pairs.
One can model any Turing Machine with a TPL Program.
Implement a TPL interpreter, hence emulate any Turing Machine, in any general purpose programming language.
Construct a "Universal Turing Machine" that is a TPL interpreter. Again, note that the UTM only has to recognize 21 input symbols.