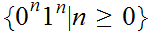Notes on Ambiguity and Pushdown Automata

An example of Ambiguity

A key example:

We showed that 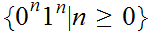cannot be recognized by a DFA.

However consider a finite automaton with a "stack." We will implement the following program:

String s;

int i=0;

if( length(s)==0) return Accept; //empty string

while ( s[i]==0){

push(s[i]);

if(i==(length(s)-1))return Reject; // all zeros

i++;

}

while ( i 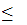(length(s)-1){

if (s[i]==1){

if (stack_empty )return Reject; // too few zeros

pop();

}

if( s[i]==0 ) return Reject; // a zero after a one

}

i++;

}

if(stack_empty )return Reject; // too many zeros

if(stack_empty )return Accept;

}

__________________________________________________

Formal Definition of a Pushdown Automaton(PDA)

A (PDA) is a 6-tuple

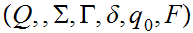, where

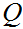• is a finite set called the states,

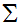• is a finite set called the input alphabet,

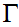• is a finite set called the stack alphabet,

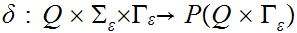• is the transition function,

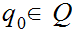• is the start state,

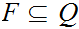• is the set of accept states.

__________________________________________________

Formal Definition of The Transition Function

The domain of the transition function 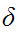are ordered triples. Each triple consists of :

• A member of 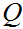, "the current state"

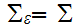
• A member of 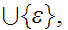"the next input symbol, (if one is to be read, else )."

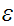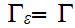
• A member of 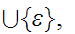"the top of the stack. (if to be popped, else 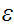if nothing is to be popped)."

The range of the transition function 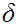are SETS of ordered pairs. Each pair of the set consists of:

• A member of 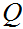, "the new state"

• The stack symbol to be pushed (may be 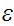if nothing is to be pushed)

________________________________________________________

Notation for PDA state diagrams

a transition 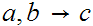is understood to mean:

• • read 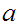from input unless 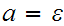In this case don't read input

  • pop 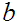from stack unles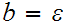s . In this case don't pop any symbols.

  • push 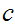onto stack unles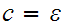s . In this case don't push any symbols

________________________________________________________

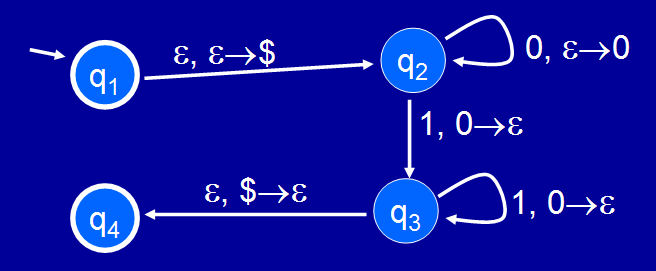
The key example: