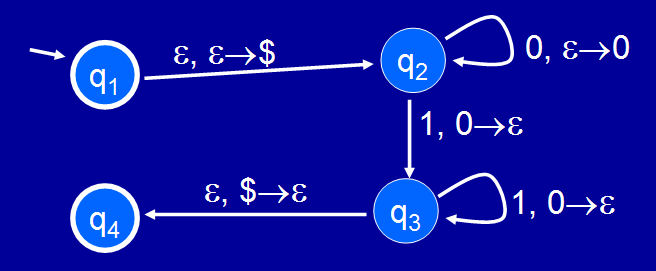
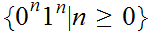 cannot be recognized by a DFA.
cannot be recognized by a DFA.
We showed that
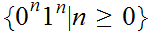 cannot be recognized by a DFA.
cannot be recognized by a DFA.
However consider a finite automaton with a "stack." We will implement the following program:
String s;
int i=0;
if( length(s)==0) return Accept; //empty string
while ( s[i]==0){
 push(s[i]);
push(s[i]);
 if(i==(length(s)-1))return
Reject; // all zeros
if(i==(length(s)-1))return
Reject; // all zeros
i++;
}
while ( i
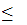 (length(s)-1){
(length(s)-1){
if (s[i]==1){
if (stack_empty )return Reject; // too few zeros
 pop();
pop();
 }
}
 if(
s[i]==0 ) return Reject; // a zero after a
one
if(
s[i]==0 ) return Reject; // a zero after a
one
 }
}
i++;
}
if(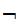 stack_empty
)return Reject; // too many zeros
stack_empty
)return Reject; // too many zeros
if(stack_empty )return Accept;
}
A (PDA) is a 6-tuple
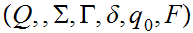 ,
where
,
where
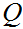 is a finite set called the states,
is a finite set called the states,
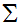 is a finite set called the input alphabet,
is a finite set called the input alphabet,
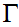 is a finite set called the stack alphabet,
is a finite set called the stack alphabet,
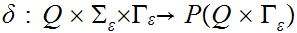 is the transition function,
is the transition function,
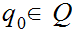 is the start state,
is the start state,
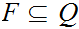 is the set of accept states.
is the set of accept states.
The domain of the transition function
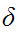 are
ordered triples. Each triple consists of :
are
ordered triples. Each triple consists of :
A member of
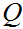 , "the current state"
, "the current state"
A member of
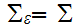
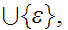 "the
next input symbol, (if one is to be read, else
"the
next input symbol, (if one is to be read, else
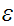 )."
)."
A member of
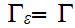
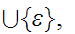 "the
top of the stack. (if to be popped, else
"the
top of the stack. (if to be popped, else
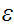 if nothing is to be popped)."
if nothing is to be popped)."
The range of the transition function
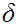 are
SETS of ordered pairs. Each pair of the set consists of:
are
SETS of ordered pairs. Each pair of the set consists of:
A member of
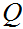 , "the new state"
, "the new state"
The stack symbol to be pushed (may be
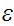 if nothing is to be pushed)
if nothing is to be pushed)
a transition
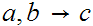 is understood to mean:
is understood to mean:
read
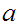 from input unless
from input unless
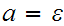 In this case don't read input
In this case don't read input
pop
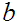 from stack unless
from stack unless
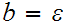 .
In this case don't pop any symbols.
.
In this case don't pop any symbols.
push
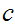 onto stack unless
onto stack unless
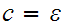 .
In this case don't push any symbols
.
In this case don't push any symbols
The key example: