Notes on Nondeterministic Finite Automata
The
Definition: If one thinks of an automaton as "a machine or control
mechanism designed to follow automatically a predetermined sequence of
operations or respond to encoded instructions" a Nondeterministic Finite
Automaton is not an automaton at all! However, a Nondeterministic
Finite Automaton can be thought of as a DFA with three defining
requirements relaxed: Specifically:
-
We allow the possibility that the transition function is not single-valued.
-
We allow the possibility that the transition function is not defined for a
given state-symbol pair.
-
We add a special symbol
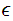 which can be thought of as "transition without reading a symbol."
which can be thought of as "transition without reading a symbol."
From the point of view of Language Recognition an NDFA is not a generalization
in the sense that every Language that is recognized by an NDFA can be
recognized by an appropriate DFA. We will give evidence of this by indicating the
appropriate modifications for the first example of a NDFA in Sipser. Before starting,
it is worth noting that the reason for introducing NDFAs is that in certain important ways
they are easier to work. In particular, it is "easier" to construct NDFAs out of components
such as in the forthcoming proof that the class of Regular Languages is closed under
concatination.
___________________________
The Example:
![$\vspace{1pt}$]()
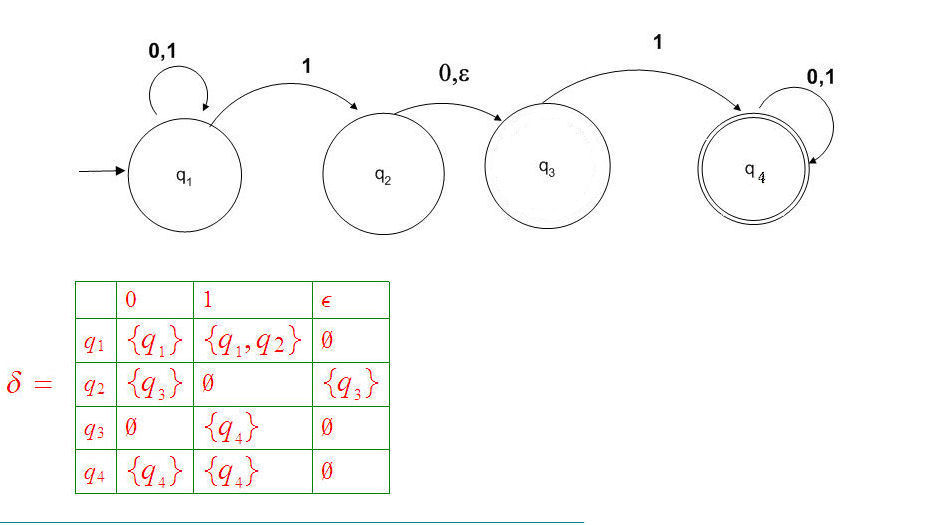
![$\vspace{1pt}$]()
_________________________________________________________________
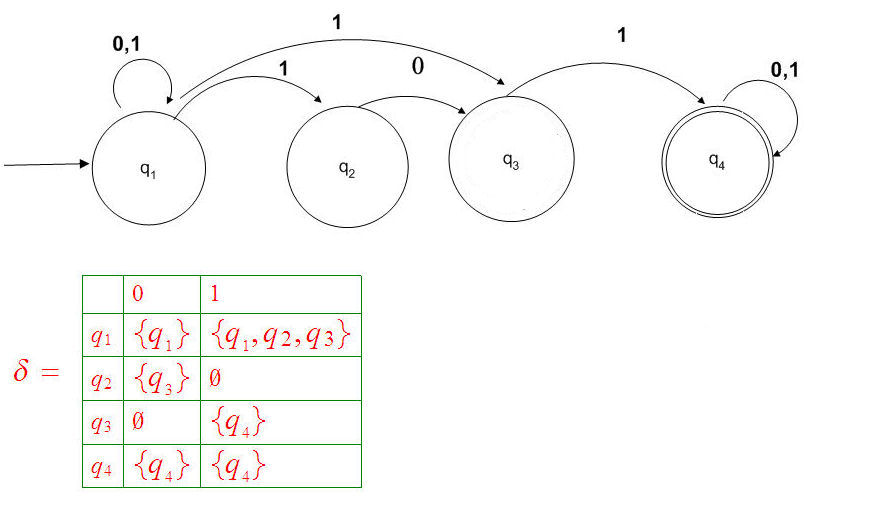
Eliminating
 :
:
![$\vspace{1pt}$]()
![$\vspace{1pt}$]()
![$\vspace{1pt}$]()
_________________________________________________________________
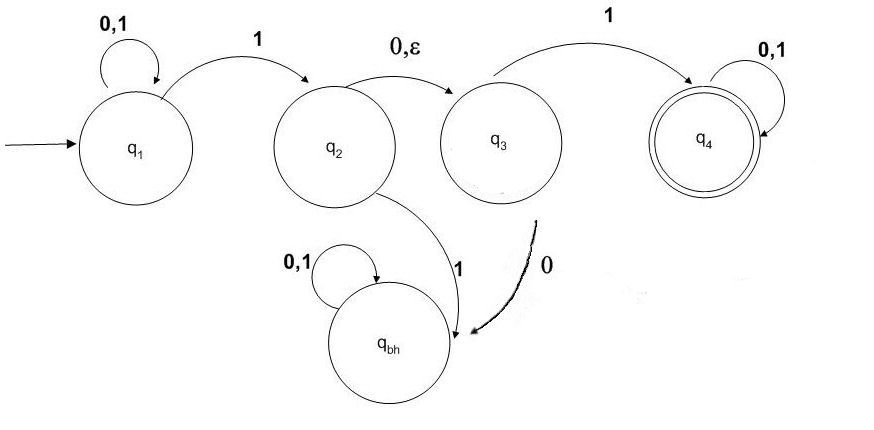
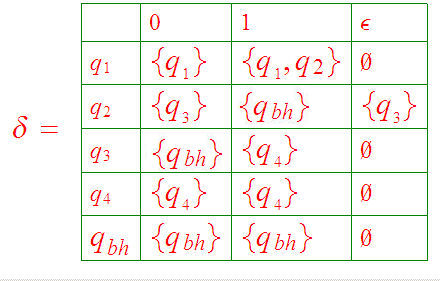
Completing the
partial transition function by adding a "black hole":
![$\vspace{1pt}$]()
__________________________________________________
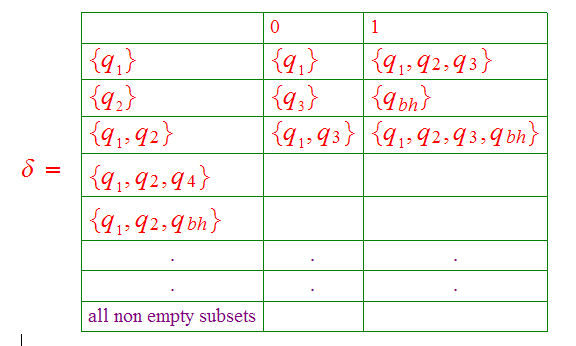
Making the
transition function single valued by adding states corresponding to ALL of the
subsets of the set of states:
_________________________________________________________________
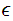 which can be thought of as "transition without reading a symbol."
which can be thought of as "transition without reading a symbol."