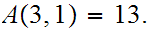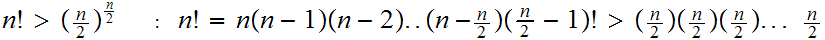 times.
times.
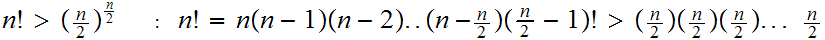 times.
times.
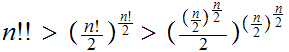
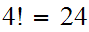
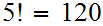
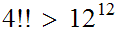
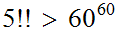
The follow version of the Ackermann function is due to Rozar Peter.
The
Ackermann-Peter
function is defined recursively for non-negative integers
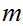 and
and
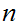 as follows:
as follows:
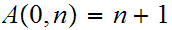
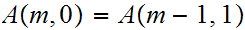
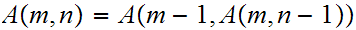
More precisely, The following method computes the Ackermann function:

The nesting in the last line leads
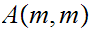 to grow much faster than
to grow much faster than
any primitive recursive function could. Here are a few values:
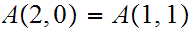
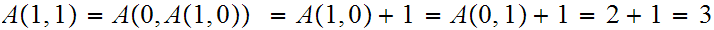
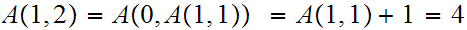
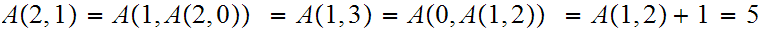
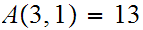
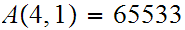
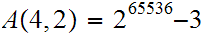
Homework Due Oct 27.
Show