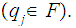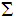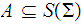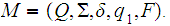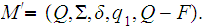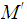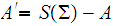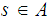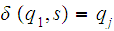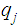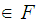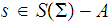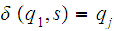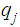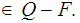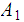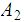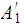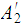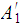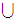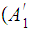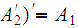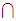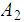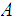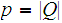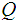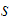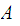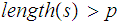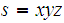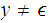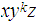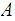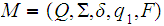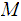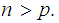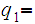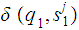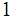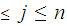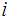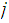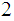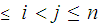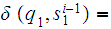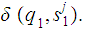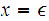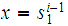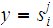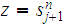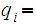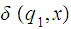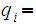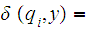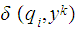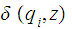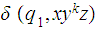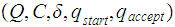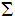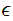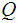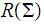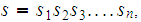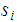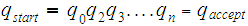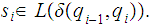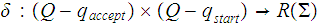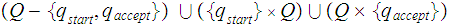Notes on
Kleene's Theorem,
The Pumping Lemma,
and
Generalized Nodeterministic Finite Automata
A
Historical Note:
That finite-state machines and regular expressions define the same class of
languages is generally know as Kleene's Theorem. Its
importance lies in the fact both descriptions provide important insights into
the nature of these languages. Regular expressions have practical applications
in computer science and finite-state machines allow us to answer general
questions about the structure of these languages.
___________________________________________________________________
String Notation:
-
Given a finite symbol set
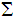 we let
we let
 be the set of strings in
be the set of strings in
 .
.
-
Given a string
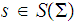 , we write
, we write
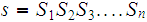 where s is the concatination of
where s is the concatination of
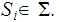
-
We write
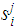 for
for
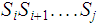 .
.
-
In this Notation, for
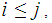
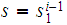
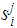
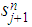 , where
, where
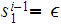 for
for
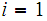 and
and
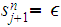 for
for
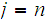 .
.
Finally,
-
Let
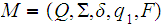 be a DFA . We can extend
be a DFA . We can extend
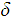 to
to
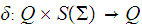 by setting
by setting
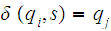 if
if
-
In this notation, the definition
 recognizes
recognizes
 can be written "
can be written "
 if and only if
if and only if
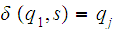 and
and
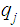 is
an accepting state
is
an accepting state
_______________________________
Lemma: The set of Regular Languages in
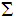 are
closed under the laws of Boolean Algebra.
are
closed under the laws of Boolean Algebra.
Proof:
Let
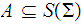 be recognized by
be recognized by
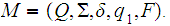 Let
Let
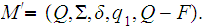 It is immediate that
It is immediate that
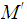 recognizes
recognizes
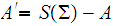
since
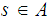 if and only if
if and only if
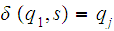 and
and
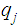
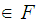 and
and
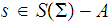 if and only if
if and only if
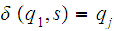 and
and
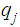
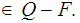
Thus if
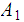 and
and
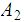 are
Regular so are
are
Regular so are
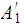 and
and
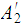 .
As is
.
As is
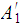
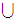
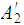 from an earlier discussion, , as is
from an earlier discussion, , as is
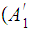
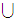
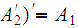
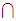
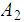 .
.
_______________________________________________
The Pumping Lemma:
states that if
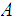 is a regular language then there is a number
is a regular language then there is a number
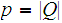 the number of states in
the number of states in
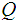 ,such
that if
,such
that if
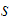 is any string in
is any string in
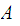 with
with
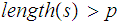 then
then
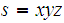 ,
the concatination of three strings, such that
,
the concatination of three strings, such that
-
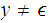
-
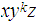 is in
is in
 for all
for all

The proof is a simple counting argument. Let
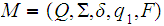 be a DFA that recognizes
be a DFA that recognizes
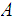 .
.
Let
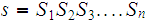 be recognized by
be recognized by
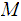 and let
and let
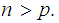 Either
Either
-
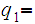
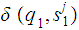 for
some
for
some
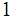
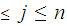
or
-
there must be an
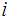 and a
and a
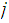 with
with
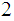
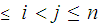 such
that
such
that
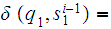
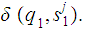
Let
To complete the argument, setting
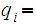
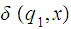 by assumption
by assumption
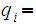
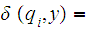 .
.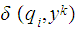 . But, also by assumption,
. But, also by assumption,
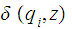 is
an accepting state so
is
an accepting state so
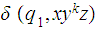 is
an accepting state.
is
an accepting state.
___________________________________________________________________
Notes on the definition of a
Generalized Nondeterministic Finite
Automaton 
-
The important generalization is that transitions are by any regular
expression, not only members of
 or
or
 .
The definition in the text is however tecnically not a generalization of a
NDFA since it is limited to a single accepting state, not equal to the start
state. NDFAs may have more than one accept state. The definition in the book
has been called a "Reduced Generalized Nonderministic Finite Automaton."
.
The definition in the text is however tecnically not a generalization of a
NDFA since it is limited to a single accepting state, not equal to the start
state. NDFAs may have more than one accept state. The definition in the book
has been called a "Reduced Generalized Nonderministic Finite Automaton."
-
It is also the case that the transition function does not take values in the
set of states
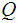 . Rather it takes values in
. Rather it takes values in
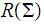 the
set of Regular Expressions over the alphabet
the
set of Regular Expressions over the alphabet
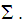 Hence
the definion of recognition must be appropriately modified. In particular,
Hence
the definion of recognition must be appropriately modified. In particular,
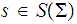 is recognized if we can write
is recognized if we can write
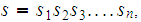 where the
where the
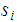 are strings, and find
are strings, and find
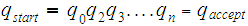 such that
such that
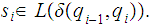 An understanding of this definition is at the hearth of an understanding of
the "State Ripping" proceedure that is used to reduce any GNFA to one with two
states.
An understanding of this definition is at the hearth of an understanding of
the "State Ripping" proceedure that is used to reduce any GNFA to one with two
states.
-
Note that
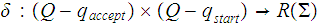 requires that there is a unique Regular expression transition
between any pair of states in
requires that there is a unique Regular expression transition
between any pair of states in
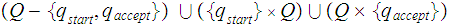 including self-transitions
including self-transitions
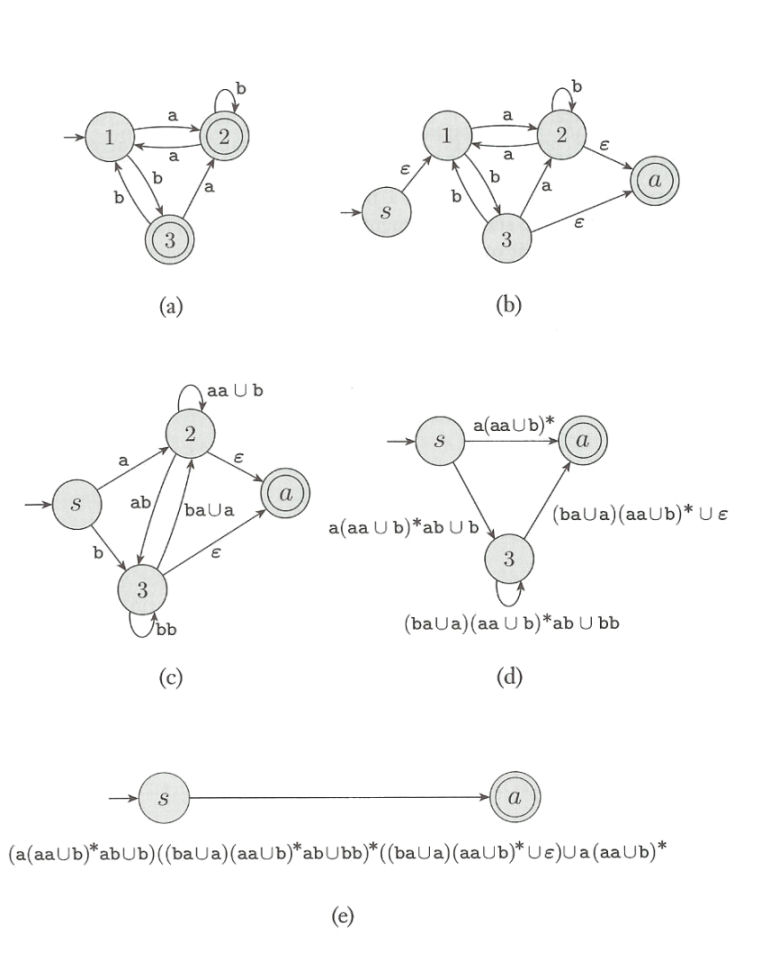
-
This diagram which was "ripped" from Van Dam's notes is at the heart of the
reduction process.

-
Note that at each stage, the reduction step is applied simultaneously all
pairs of states that are part of the reduced automaton.
-
That the reduced automaton recognizes the same Language follows easily from
definition 2. above
-
This diagram is from the text. Homework: Due Sept 20 Problem
1.21 (b)
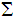 we let
we let
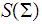 be the set of strings in
be the set of strings in
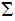 .
.
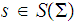 , we write
, we write
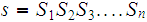 where s is the concatination of
where s is the concatination of
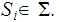
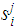 for
for
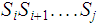 .
.
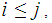
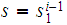
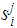
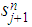 , where
, where
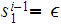 for
for
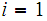 and
and
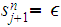 for
for
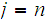 .
.
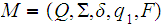 be a DFA . We can extend
be a DFA . We can extend
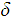 to
to
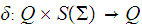 by setting
by setting
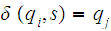 if
if
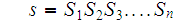
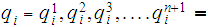
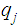 such
that
such
that
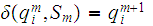 for
all
for
all
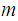 .
.
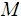 recognizes
recognizes
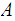 can be written "
can be written "
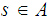 if and only if
if and only if
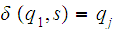 and
and
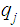 is
an accepting state
is
an accepting state