

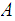 is not a CFL.
is not a CFL.
choose
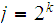 large enough so that , by the CFL pumping lemma,
large enough so that , by the CFL pumping lemma,
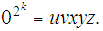
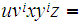
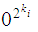 with
for all
with
for all
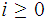 and some
and some
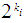 .
.
Moreover,
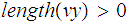
Let
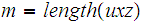 and
and
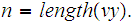
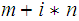
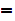
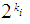 , some
, some
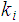 , for all
, for all
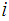 .
However this is not possible since
.
However this is not possible since
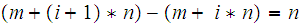 , a constant and
, a constant and
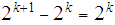 . In particular the sequence
. In particular the sequence
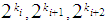 ,
is not constant.
,
is not constant.
Check if
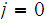 or
or
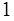 . If
. If
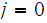 reject. If
reject. If
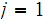 accept.
accept.
Check, by going left to right if the string has even or odd number of zeros
If odd then "reject"
If even then go back left, erasing half the zeros.
goto 1.
