0.1 Complexity Theory

- Moore's Law

0.1.1 Moore's Law

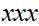
Moore's Law can provide a framework for discussing two superficially different situations:

We would like to do a computation, but lack computers of sufficient power for the required datasets. We want to know when these computations will be possible. Using current technology, we can do the computation for "smaller" datasets.
We do not want others to be able to do a certain computation, for example breaking some encryption methodology. We need to estimate when the necessary compute-power might be available.

0.1.2 Two Loosely Drawn Examples

Addition

Consider the following template for addition

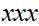
$\QTR{Large}{xxx}$

$\QTR{Large}{zzz}$

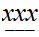
Setting aside carries, it requires 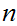$\QTR{Large}{n}$ addition table lookups to add to 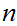$\QTR{Large}{n}$ digit numbers. That is, if it is practical to add two 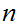$\QTR{Large}{n}$ digit numbers today, in eighteen months it will be practical to add two 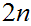$\QTR{Large}{2n}$ digit numbers.

Multiplication

Consider the following template for addition

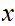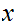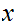$\QTR{Large}{x}$ $\QTR{Large}{x}$ $\QTR{Large}{x}$

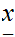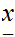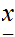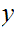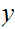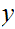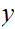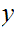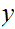$\QTR{Large}{y}$ $\QTR{Large}{y}$ $\QTR{Large}{y}$

$\QTR{Large}{y}$ $\QTR{Large}{y}$ $\QTR{Large}{y}$

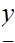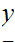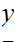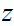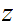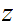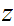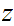$\QTR{Large}{z}$ $\QTR{Large}{z}$ $\QTR{Large}{z}$ $\QTR{Large}{z}$ $\QTR{Large}{z}$

Again, setting a lot of arithmetic , it requires 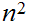multiplication table lookups to multiply to 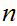$\QTR{Large}{n}$ digit numbers. That is, if it is practical to multiply two 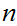$\QTR{Large}{n}$ digit numbers today, in three years it will be practical to multiply two 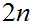$\QTR{Large}{2n}$ digit numbers.

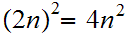
so we will have to do 4 times as many operations.

0.1.3 One Loosely Stated Definition

Another way to gain compute-power is to increase the number of processors in a given computer. Then, assuming we could do a lot of processing in parallel, we would not have to wait the time predicted by Moore's Law to get faster processors. However there are practical limitations to this approach that have to be considered. Moreover, neither Moore's Law nor parallel processing are really part of this course. So, very informally, we will use the term "Moore cycle" to refer to the engineering cycle, or expense, or whatever, it takes to produce a computer capable of doing twice as many operations in the same time period.

Stated in these terms, it takes one Moore cycle to double the number of digits we can add and two Moore cycles to double the number of digits we can multiply. Going back to the two situations mentioned in 0.1.1, from a planning perspective, doubling the number of digits involving either addition or multiplication is not "hard."

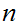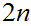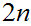To be slightly more concrete, if I had an encryption system that depended on multiplication. Suppose that today I could break that system when $\QTR{Large}{n}$ digits were involved but not $\QTR{Large}{2n}$ . The life-span of safe " $\QTR{Large}{2n}$ "- encryption would be very short!

		$\QTR{Large}{x}$	$\QTR{Large}{x}$	$\QTR{Large}{x}$

		$\QTR{Large}{y}$	$\QTR{Large}{y}$	$\QTR{Large}{y}$
	$\QTR{Large}{y}$	$\QTR{Large}{y}$	$\QTR{Large}{y}$

$\QTR{Large}{z}$	$\QTR{Large}{z}$	$\QTR{Large}{z}$	$\QTR{Large}{z}$	$\QTR{Large}{z}$