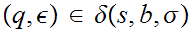For every CFG
 ,
there is a PDA
,
there is a PDA
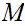 with
with
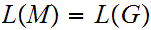 .
.
For every PDA
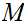 ,
there is a CFG
,
there is a CFG
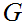 with
with
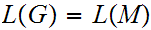 .
.
For every CFG
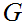 ,
there is a PDA
,
there is a PDA
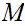 with
with
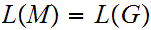 .
.
For every PDA
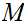 ,
there is a CFG
,
there is a CFG
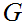 with
with
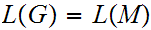 .
.
Every CFL language is accepted by some PDA.
Let
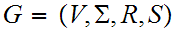 be the CFL in Chomsky Normal Form.
be the CFL in Chomsky Normal Form.
1. The corresponding PDA has the following states:
A start states
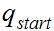 and a secondary start state
and a secondary start state
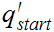
A main "loop" state
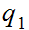 and additional states
and additional states
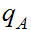 , for every
, for every
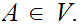
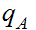 will
be used to "push productions" of the form
will
be used to "push productions" of the form
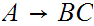 onto the stack.
onto the stack.
An accept state
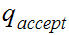
2. The
input alphabet is
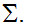
3. The stack alphabet
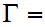
 , where
, where
 is some new nonterminal.
is some new nonterminal.
4. The transition rules are:
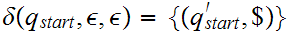 and
and
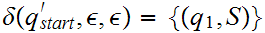
That is, push
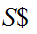 onto
the stack.
onto
the stack.
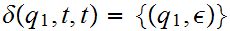 for all
for all
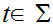
That is pop terminals from the stack if they match the next input symbol. Note; If you see non-matching terminals...failure no rule!
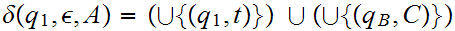 for all rules of the form
for all rules of the form
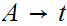 ,
,
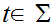 and all rules of the form
and all rules of the form
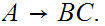
Either replace
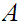 with some appropriate
terminal
with some appropriate
terminal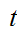 , or begin replacing
, or begin replacing
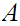 with
with
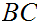 on the top of the stack.
on the top of the stack.
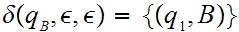 for all
for all
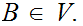
Push the other nonterminal in the "Chomsky Production"
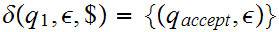
Pop the last symbol on the stack and go to the accept state.
Example: To be done in class:
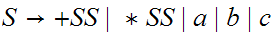
A Chomsky Version:
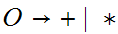
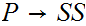
Homework Due October 20
a. Problem 2.10 Page 129 from the Text.
b. Apply the above method to find a PDA equivalent to
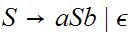 .
.
Every PDA language is accepted by some CFL.
Some assumptions:
We can always find an equivalent PDA
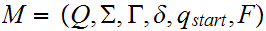 such that:
such that:
There is a single accept state ,
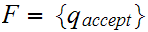
The stack is empty when a string is accepted.
Every stack operation is either a push or a pop. That is there are no replacement operations.
We now construct G:
Add Variables:
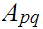 for all pairs
for all pairs
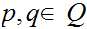 .
.
Let
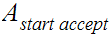 be the start variable.
be the start variable.
Production Rules:
For all pairs
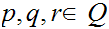 ,
add the rule
,
add the rule
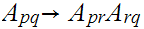 .
.
For all
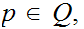 add the rule
add the rule
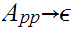
For states
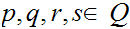 and
and
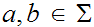 add the rule
add the rule
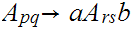
if
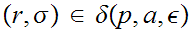 and
and