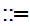
"Backus-Naur Form (BNF)" is the term attributed to a standard formal notation used to describe the syntax of programming languages. The notation is based on the work of John Backus and that of Peter Naur. We briefly review BNF as background for the study of Automata and Languages .
_________________________________________________________________________________
The meta-symbols of BNF are:
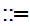
meaning "is defined as"
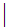
meaning "or"
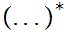
meaning zero or more occurences of ......

meaning zero or one occurence of ......
Moreover,
 ,angle brackets, are used to distinguish non-terminal symbols from terminal
symbols which are written exactly as they are to be represented.
,angle brackets, are used to distinguish non-terminal symbols from terminal
symbols which are written exactly as they are to be represented.
A BNF rule defining a nonterminal has the form:
nonterminal
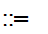 a
sequence consisting of strings of
a
sequence consisting of strings of
terminals
or nonterminals separated by the meta-symbol
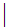
Here are some examples:

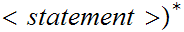
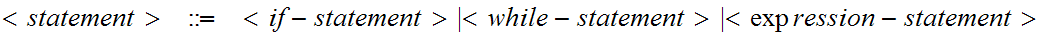
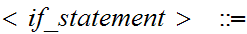 if
(
if
(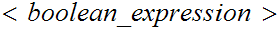 ){
){
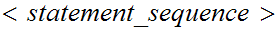
 }else{
}else{
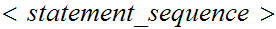 }]
}]
}
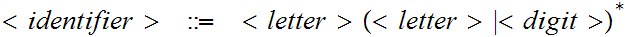
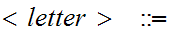 a
a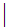 b
b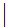 c
c
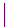 d
d
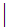 ......
......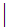 A
A B
B C
C .....
.....
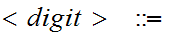 0
0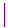 1
1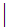 ....
....
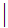 8
8
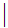 9
9
______________________________________________________________________
Example : a2H
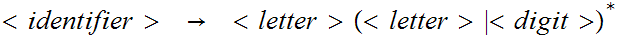
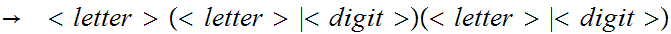
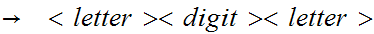
.
.
 a2H
a2H